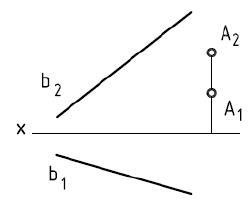
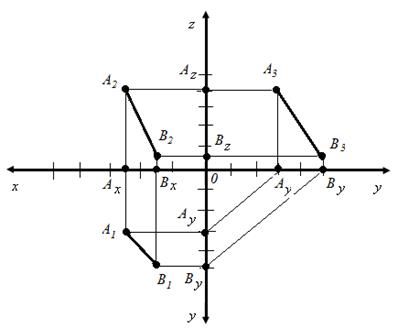
Pentru a găsi proiecția orizontală A1 a punctului A, trasăm valoarea x = 25mm de la origine în direcția pozitivă a axei Ox (de la punctul 0 la stânga) și determinăm punctul AX. iar pe direcția pozitivă a axei Oy se compară valoarea y = 30 (de la punctul 0 în jos) și se determină poziția punctului AV.
Intersecția perpendicularilor trase prin punctele AX și AU către axele corespunzătoare Ox și Oy va indica poziția proiecție orizontală a punctului A1.
Știind că proiecția orizontală a vizualizării față A1 și A2 se află pe aceeași linie de comunicare, care este perpendiculară pe axa Ox, iar proiecția frontală la distanță de axa Ox de suma applicate z = 40, determinăm poziția proiecția frontală a punctului A, și anume A2. Front A2 profil de proiecție de proiecție și A3, de asemenea, se află pe aceeași linie de comunicare, care este perpendiculară pe axa Oz, iar proiecția profilului este îndepărtat din axa Oz coordona valoarea la y = 30.
În mod similar, găsim poziția proiecțiilor orizontale, frontale și de profil ale punctului B.
Având conectat A1 cu B1. obținem o proiecție orizontală a segmentului AB, A2 și B2, proiecția frontală a segmentului și A3 cu B3 proiecția profilului segmentului (Figura 9).
Numărul sarcinii 3. Determinați valoarea reală a segmentului AB și unghiurile de înclinare ale acestuia față de planurile proeminențelor П1. P2 și P3.
Valoarea intervalului natural, situată pe o linie dreaptă în poziția generală, este ipotenuza unui triunghi dreptunghic cu cateta din care este o proeminență pe una dintre planurile proeminentelor, iar celălalt - punctele finale diferență distanța față de același plan.
Unghiul dintre piciorul de proiecție și hypotenuse al unui triunghi cu unghi drept este egal cu valoarea reală a unghiului de înclinare al segmentului față de planul proiecțiilor pe care sunt construite construcțiile.
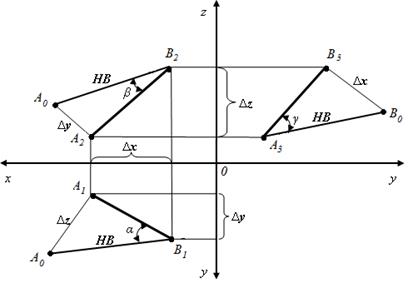
1. În figura 10, lungimea segmentului AB și unghiul a constituit de linia AB cu planul P1. sunt definite dintr-un triunghi drept, care este construit după cum urmează:
1.1. Proiecția orizontală a segmentului AB-A1 B1 este un picior al triunghiului. Din orice punct al acestui picior (din punctul A1 sau B1) tragem o linie dreaptă, perpendiculară pe A1 B1.
1.2. Determinăm diferența dintre coordonatele z pentru punctele A și B (zB - zA = Dz) - acesta este al doilea picior al triunghiului drept, l-am lăsat din punctul A și am obținut punctul A0.
1.3. Ipotenuză A0 B1 este valoarea reală a segmentului AB și unghiul a, închis între orizontală lungimea de proiecție A1 și B1 valoarea reală a acestui segment este unghiul de înclinare a segmentului AB la planul P1.
2. în figura 10, lungimea segmentului AB și unghiul format de linia AB cu planul P2. sunt determinate dintr-un triunghi drept construit pe proiecția frontală A2 B2 cu al doilea picior A2 A0. egală cu diferența dintre coordonatele y pentru punctele A și B (yA - yB = Dy).
Ipotenuză A0 și B2 este valoarea reală a segmentului AB, iar unghiul b, închis între lungimea de proiecție frontală A2 și B2 valoarea reală a segmentului AB este un unghi segment la un plan P2.
3. în figura 10, lungimea segmentului AB și unghiul g format de linia AB cu planul N3. sunt determinate dintr-un triunghi drept construit pe proiecția profilului A3B3 cu al doilea picior В3 В0. egală cu diferența coordonatelor x pentru punctele A și B (xA - xB = Dx).
Ipotenuză A3 B0 este valoarea reală a segmentului AB, iar unghiul g, închis între lungimea A3 profil de proiecție și B3 valoarea reală a segmentului AB este un unghi segment la P3 avionul.
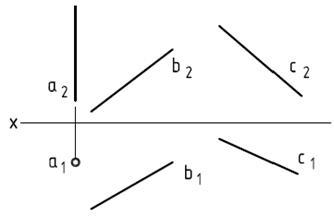
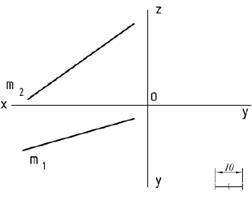
2.7. Construiți proiecțiile punctelor care aparțin liniei drepte m: A - o distanță de 25 mm față de planul П1. B - 15 mm distanță de planul P2. C - distanță la distanță egală cu planurile П1 și П2. Câte soluții sunt posibile?
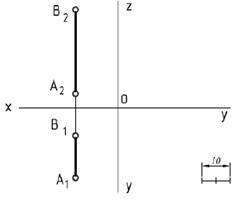
2.8. Construiți proiecțiile punctului C aparținând segmentului AB și distanțate de planul П1 la 15 mm.
2.9. Construiți proiecțiile unei linii drepte paralele cu planul P1 care trece prin punctul A și se intersectează linia b.
2.10. Construiți proiecțiile unei linii drepte paralele cu linia dreaptă c și intersectând liniile a și b.