Formulele plus sunt folosite pentru a exprima prin sinus și cosinus ale unghiurilor a și b, valorile funcțiilor cos (a + b), cos (a-b), sin (a + b), sin (a-b).
Formulele de adiție pentru sines și cosinus
Teoremă: Pentru orice a și b, următoarea ecuație este valabilă: cos (a + b) = cos (a) * cos (b) - păcat (a) * sin (b).
Să dovedim această teoremă. Luați în considerare următoarea figură:
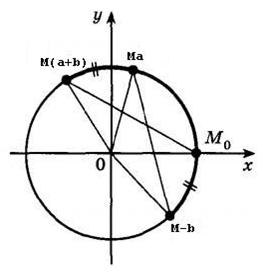
Pe aceasta, punctele Ma, M-b, M (a + b) sunt obținute prin rotirea punctelor Mo în unghiurile a, b și a + b, respectiv. Din definițiile sinus și cosinus coordonatele acestor puncte vor sleyuuyuschimi: Ma (cos (a); sin (a)), Mb (cos (-b) sin (-b)), M (a + b) (cos (a + b), păcatul (a + b)). UgolMoOM (a + b) = ugolM-boma triunghiuri egale, prin urmare, moom (a + b) și M-Boma, în care acestea sunt isoscel. Deci, bazele lui MoM (a-b) și M-bMa sunt de asemenea egale. Prin urmare, (MoM (a-b)) ^ 2 = (M-bMa) ^ 2. Folosind formula pentru distanța dintre două puncte, obținem:
(A + b)) 2 + (sin (a + b)) ^ 2 = (cos (-b) -cos (a) ) ^ 2.
sin (-a) = -sin (a) și cos (-a) = cos (a). Ne transformăm ecuația cu aceste formule și cu pătratul sumei și diferenței, atunci:
1 2 cos (a + b) + (cos (a + b)) ^ 2 + (sin (a + b)) ^ 2 = cos (b) (a) + (cos (a) ^ 2 + (sin (b)) ^ 2 + 2 * sin (b) * sin (a) + (sin (a)).
Acum aplicăm identitatea trigonometrică de bază:
2 2 * cos (a + b) = 2 - 2 * cos (a) * cos (b) + 2 * sin (a) * sin (b).
Vom cita altele similare și le vom reduce cu -2:
cos (a + b) = cos (a) * cos (b) - sin (a) * sin (b). După cum este necesar pentru a dovedi.
Următoarele formule sunt, de asemenea, valabile:
Aceste formule pot fi obținute din cele de mai sus, utilizând formulele de reducere și înlocuind b cu -b. Pentru tangente și cotangente există și formule de adăugare, dar ele nu vor fi valabile pentru argumente.
Formule pentru adăugarea de tangente și cotangente
Pentru orice unghi a, b cu excepția a = pi / 2 + pi * k, b = pi / 2 + pi * n și a + b = pi / 2 + pi * m, pentru toate numerele întregi k, n, m va avea următoarele formula:
tg (a + b) = (tg (a) + tg (b)) / (1-tg (a) * tg (b)).
Pentru orice unghi a, b cu excepția a = pi / 2 + pi * k, b = pi / 2 + pi * n și a-b = pi / 2 + pi * m, pentru toate numerele întregi k, n, m va avea următoarea formulă:
Pentru orice unghi a, b, cu excepția a = pi * k, b = pi * n, a + b = pi * m și pentru oricare întregi k, n,
ctg (a + b) = (ctg (a) * ctg (b) -1) / (ctg (b) + ctg (a)).
Pentru orice unghi a, b, cu excepția a = pi * k, b = pi * n, a-b = pi * m și pentru oricare întregi k, n,
ctg (a-b) = (ctg (a) * ctg (b) +1) / (ctg (b) -ctg (a)).