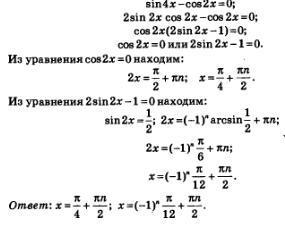Gama de aplicare a formulelor de adiție este destul de largă. Nu ne propunem să enumerăm toate variantele posibile de aplicare a formulelor de completare, aici ne uităm doar la modul în care aceste formule sunt aplicate în practică.
În primul rând, utilizând una dintre formulele de adăugare, permiteți-ne să verificăm formula de reducere pentru specie. Folosim sinusul sumei. Avem. Deci formula este dovedită.
Formulele de adăugare vă permit să calculați valorile exacte ale sinusurilor, cosinusului, tangentei și cotangentelor unor unghiuri diferite de cele de bază. Luați în considerare soluția exemplului.
Calculați valoarea exactă a tangentei de 15 grade.
Este ușor de observat că un unghi de 15 grade poate fi reprezentat ca o diferență de 45-30. Apoi, formula de diferență tangentă ne va permite să calculam valoarea necesară. Prin formula de mai sus, obținem. Acum înlocuim valorile cunoscute ale tangentei, după care finalizăm calculele:

.
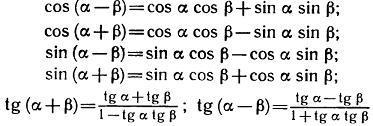
De exemplu, trebuie să determinați sinus, cosinus, tangent sau cotangent de orice unghi de la 0 la 450 de grade:
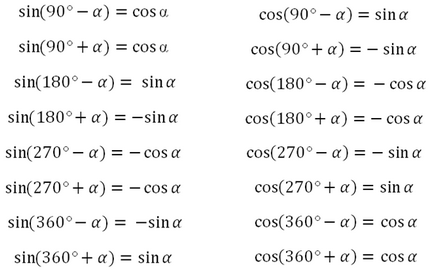
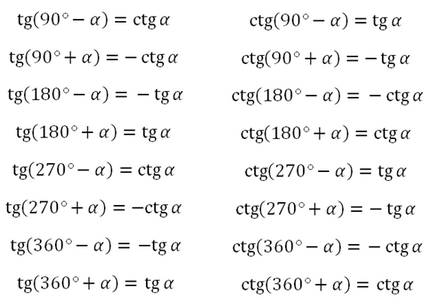
Unghiul alfa se situează între 0 și 90 de grade
Deci, este necesar să înțelegem "legea" care funcționează aici:
1. Determinați semnul funcției în trimestrul corespunzător.
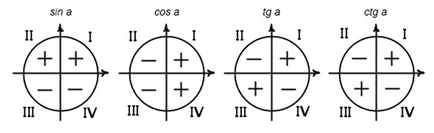
2. Rețineți următoarele:
funcția este schimbată la o funcție
(sine la cosinus sau invers, tangent la cotangent sau invers)
funcția nu se schimbă în funcție
Acum, conform legii prezentate, vom scrie noi înșine câteva formule ale reducerii:
Acest unghi se situează în al treilea trimestru, cosinusul în al treilea trimestru este negativ. Nu schimbăm funcția de cooperare, deoarece avem 180 de grade, înseamnă:
Unghiul constă în al treilea trimestru, cosinusul în trimestrul al treilea este negativ. Schimbăm funcția în funcție, deoarece avem 270 de grade, înseamnă:
Unghiul constă în primul trimestru, sinusul în primul trimestru este pozitiv. Nu modificați funcția în funcție, deoarece avem 360 de grade, înseamnă:
Aici aveți o confirmare suplimentară că sinusurile unghiurilor adiacente sunt egale:
§ 24. Formulele dublei argumente
Aici vom discuta formulele trigonometrice care ne permit să exprimăm aceste formule. Aceste formule sunt denumite de obicei formulele cu dublu argument. Este posibil ca titlul să nu fie foarte reușit, așa cum sunt, de asemenea, nume precum "formule de reducere", "sinus de sumă", "cosinus de diferență" etc., dar acest lucru nu este important: principalul lucru este că există un simbol verbal , permițând inițiaților să înțeleagă ceea ce este în joc.examinează expresia sin2x, reprezentând 2x în forma x + x, care ne permite să aplicăm expresia sinus de sumă expresiei păcat (x + x) (vezi §21). Avem:
Luați în considerare expresia cos2x, reprezentând 2x în forma x + x. Aceasta ne permite să aplicăm expresia cos (x + x) (a se vedea §21) formula "cosinusul sumei". Avem:
Luați în considerare expresia tan 2x, reprezentând 2x în forma x + x. Aceasta ne permite să aplicăm formula "tangentă sumă" la expresia tg (x + x) (a se vedea §23). Avem:
Formula „argument sinus dublu“ și „cosinus dublu argument“ valabil pentru orice valori argument (fără restricție), în timp ce formula „dublu argument tangent“ valabil numai pentru acele valori ale argumentului x, care sunt definite tg x și tg 2 X și Numitorul fracției este, de asemenea, nenul; Desigur, formulele cu două argumente pot fi folosite și în cazul în care locul argumentului x are o expresie mai complexă. Astfel, au următoarele relații:
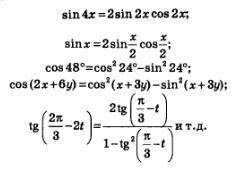
Exemplul 1. Dovediți identitățile:
Soluție: a) Folosim faptul că 1 = sin 2 x + cos 2 x și formula sine a argumentului dublu. Avem:
Exemplul 2. Reduceți fracțiunea Soluție. În numerotatorul fracțiunii, folosim identitatea, demonstrată în Exemplul 1 și în numitor prin formula cosinus a argumentului dublu. Avem:
Exemplul 3. Calculați: Soluție: a) Expresia specificată este partea dreaptă a formulei cosinuse a argumentului dublu. Observând asta, ajungem
b) Expresia specificată este partea dreaptă a sinusului argumentului dublu, dar lipsește numai factorul 2. Introducând-o, obținem:
c) Acest exemplu este mult mai complicat, dar este mai frumos decât cele precedente: aici trebuie să ghiciți să multiplicați și să împărțiți expresia dată cu 4 cos 18 °. Ce va da? A se vedea:
După cum puteți vedea, am folosit de două ori formula forțată a unui argument dublu. Pentru a finaliza calculele, rețineți că 72 ° = 90 ° -18 °. Aceasta înseamnă că păcatul 72 0 = sin (90 ° -18 0) = cos 18. Astfel,
Exemplul 4. Dovediți soluția de identitate. Transformăm partea de stânga a identității care trebuie dovedită:
Înmulțind atât numerotatorul, cât și numitorul ultimei fracții cu 2 ("ajustarea" numitorului la formula sine a argumentului dublu), obținem:
Deci, după cum este necesar. Încă o dată, atragem atenția asupra faptului că identitatea este demonstrată numai pentru valoarea admisibilă a lui x, mai exact pentru valorile lui x pentru care numitorii sunt diferiți de zero.
Soluția: a) Folosim formula sin sin 2 x + cos 2 x = 1. Avem:
b) Pentru a calcula sin2x, folosim formula sin sinx 2x = 2 sin x cos x. Valoarea cos x este dată în condiție, iar valoarea păcatului x se găsește după cum urmează. În primul rând, știm deja că în al doilea rând, prin ipoteză, argumentul x aparține trimestrului al patrulea și în el sinusoidul este negativ. Aceasta înseamnă că din două valori
c) tg2x se calculează folosind definiția tangentei:
d) Pentru calcul, mai întâi folosim formula de reducere: Aplicăm formula cosinusului argumentului dublu la expresia cos4x: cos4x = cos2 2x - sin2 2x. Folosim faptul că valorile cos 2x și păcat 2x au fost deja găsite de noi:
Exemplul 6. Rezolvați ecuația sin4x-cos3x = 0. Soluția. Dacă formula sinusală a argumentului dublu este aplicată expresiei sin4x în partea stângă a ecuației, atunci partea stângă poate fi descompusă în multiplicatori. Avem în serie: