Magic. sau un pătrat magic este o masă pătrată umplută cu n 2 numere, astfel încât suma numerelor din fiecare rând, fiecare coloană și ambele diagonale să fie aceleași. Dacă într-un pătrat sumele de numere sunt egale numai în rânduri și coloane, atunci se numește semi-magică. Normal este un pătrat magic plin cu întregi de la 1 la n 2. Un pătrat magic este numit asociativ sau simetric. dacă suma oricăror două numere aranjate simetric față de centrul pătratului este n 2 + 1.
Pătratele magice normale există pentru toate ordinele, cu excepția n = 2. Cu toate că cazul n = 1 este trivial - pătratul este format dintr-un singur număr. Cazul minimal trivial este prezentat mai jos, este de ordine 3.
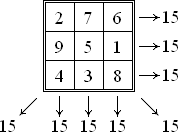
Suma numerelor din fiecare rând, coloană și diagonală se numește constanta magică. M. Constanta magică a unui pătrat magic magic depinde numai de n și este definită de formula
Primele valori ale constantelor magice sunt date în tabelul următor (secvența A006003 în OEIS):
Suma numerelor în orice orizontală, verticală și diagonală egală cu 34. Această sumă se regăsește în toate colțurile pătrat 2 x 2 într-un pătrat centrală (10 + 11 + 6 + 7), pătrat celulelor de colț (16 + 13 + 4 + 1 ) în pătrate construite "calul leagăn" (2 + 8 + 9 + 15 și 3 + 5 + 12 + 14), în dreptunghiurile formate din perechile de celule secundare pe laturile opuse ale (3 + 2 + 15 + 14 și 5 + 8 + 9 + 12). Majoritatea simetriilor suplimentare se datorează faptului că suma a două numere centralizate aranjate simetric este de 17.
Pătraturile lui Henry E. Dyudeni și Allan W. Johnson-Jr.
Dacă matricea pătrată n × n nu este strict un număr natural de numere, atunci acest pătrat magic este neconvențional. Mai jos sunt două pătrate magice, pline de numere prime. Primul are ordinul n = 3 (Piața Dyudeni); Al doilea (dimensiunea 4x4) este pătratul Johnson. Ambele au fost dezvoltate la începutul secolului al XX-lea [6]:
Există mai multe astfel de exemple:
Ultimul pătrat, construit în 1913 Dzh.N.Mansi, este remarcabil prin aceea că acesta este compus din 143 de numere prime consecutive, cu excepția a două lucruri: unitatea în cauză, care nu este un număr prim, și nu sunt folosite doar un prim chiar numărul 2.
Pătraturi cu proprietăți suplimentare
Piața magică a diavolului
Devil Magic pătrat - pătrat magic, care coincide, de asemenea, cu suma constantă magică a numerelor de diagonală rupte (diagonală, care sunt formate prin plierea unui pătrat în torr), în ambele direcții.
Astfel de pătrate sunt numite pandiagonal.
Există 48 de pătrate magice diabolice de 4 × 4 exacte pentru rotații și reflecții. Dacă luăm în considerare și traducerile lor paralele simetrice, vor exista doar 3 pătrate în esență diferite:
Construirea de pătrate magice
Este chiar mai ușor să faceți construcția în felul următor. Se ia matricea n x n. În interiorul acestuia este construit un diamant în trepte. În ea, celulele din stânga în diagonală sunt umplute cu o serie de numere impare. Se determină valoarea celulei centrale C. Apoi, în colțurile pătratului magic, valorile vor fi: celula dreaptă superioară C-1; celula inferioară din stânga C + 1; celula inferioară dreaptă C-n; partea stângă superioară C + n. Umplerea celulelor goale în triunghiuri treptate se efectuează cu respectarea regulilor simple: 1) pe liniile de număr de la creșterea stânga la dreapta în etapa n + 1; 2) pe coloanele de sus în jos, numerele cresc în incremente de n-1.
algoritmi pentru construirea pătrate pandiagonalnyh, [14] [15], de asemenea, și pandiagonalnyh și asociative patrate de 9x9 magice au fost de asemenea dezvoltate. [16] [17] Aceste rezultate ne permit să construim pătrate magice ideale de ordine n = 9 (2k + 1) pentru. [9] [18] Există, de asemenea, o metodă comună de dispunere ideală pătrate magice de ordine impar n> 3. [19] O metodă de construire pătrate magice ideale de ordinul n = 8k, k = 1,2,3. [20] Pătraturile pandiagone de ordin ordonat pot fi combinate numai dacă acestea sunt neconvenționale. [21] [22] [23]. Cu toate acestea, se pot găsi pătrate aproape pandiagonalnye [24] Există un grup special ideal pătrate magice perfecte (convenționale și neconvenționale) [25].
Exemple de pătrate mai complexe
Practic elaborate din punct de vedere tehnic, pătrate magice de ordin ciudat și ordinea parității duble. [26] Formalizarea pătratelor de ordinul unei singure parități este mult mai dificilă, după cum ilustrează următoarele scheme:
Există câteva duzini de alte metode pentru a construi pătrate magice
Modificarea șahului
Se știe că șahul. ca și pătratele magice, au apărut cu zeci de secole în urmă în India. Prin urmare, nu a fost întâmplător faptul că a apărut ideea unei abordări de șah la construirea unor pătrate magice. Pentru prima dată acest gând a fost exprimat de Euler. El a încercat să obțină o pătrată magică completă trăgând continuu calul. Totuși, acest lucru nu a reușit, deoarece în diagonalele principale sumele de numere diferă de constanta magică. Cu toate acestea, defalcarea șahului vă permite să creați orice pătrat magic. Cifrele se umple în mod regulat și se trasează liniar cu culoarea celulelor.
Imagine a schemelor de construire a patratelor magice.