2. Privire de ansamblu asupra modulului imgproc al bibliotecii OpenCV
2.1. Convoluții și filtre liniare
Filtrele liniare sunt o familie a celor mai simple filtre de imagine în termeni de descriere matematică [6]. Să presupunem că există o imagine în semifinală. Apoi orice filtru liniar este definit de funcția reală dată pe raster. Această funcție se numește kernelul de filtrare. iar operația de filtrare se realizează prin calcularea unei convoluții discrete:
Ca regulă, kernelul de filtrare este aplicat în unele cartiere ale punctului 0, astfel încât limitele modificărilor indexului sunt determinate de forma selectată și dimensiunea cartierului. Acest cartier din anumite surse este numit șablon sau diafragmă. În procesul de calcul al convoluției, pixelii sunt trecuți prin întreaga imagine, modelul este suprapus pe fiecare pixel curent prin combinarea pixelului cu un anumit punct al șablonului - poziția de bază a șablonului. după care se calculează convoluția. Este necesar să acordăm o atenție specială situației în care pixelul curent se află la marginea imaginii. Această problemă poate fi rezolvată în mai multe moduri:
- Îndepărtați marginile, adică Nu filtrați pentru toți pixelii de graniță că nu puteți aplica un șablon fără a lăsa imaginea.
- Nu luați în considerare în procesul de sumare un pixel care nu există în realitate.
- Pentru a defini vecinătatea pixelilor de graniță prin extrapolare (de exemplu prin simpla dublare a pixelilor delimitate).
- Pentru a defini vecinătatea pixelilor de graniță prin intermediul reflexiei speculare, adică înfășurați imaginea în torus.
Alegerea soluției depinde în mare măsură de aplicarea, de exemplu, imaginea oglindă în practică nu este chiar o modalitate naturală.
Pentru a calcula pachetele din biblioteca OpenCV, există o funcție filter2D.
Să analizăm în detaliu parametrii funcției reduse.
- src este imaginea originală.
- dst - convoluție. Are același număr de canale și o adâncime ca imaginea originală.
- ddepth - adâncimea imaginii rezultate. Dacă o valoare negativă este trecută la intrarea funcției, adâncimea este aceeași cu adâncimea imaginii de intrare.
- kernel - kernel convolution, matrice reală cu un singur canal.
- ancora este poziția de lider a kernel-ului. Valoarea implicită este (-1, -1), ceea ce înseamnă că poziția de lider este situată în centrul kernel-ului.
- delta este o constantă care poate fi adăugată la valoarea intensității după filtrare înainte de a scrie rezultatul direct.
- borderType este un parametru care definește metoda de adăugare a frontierei, astfel încât să puteți aplica un filtru pixelilor limitați ai imaginii originale. Acceptă orice valoare a formularului BORDER_ * cu excepția BORDER_TRANSPARENT și BORDER_ISOLATED.
Funcția oferă aplicarea unui filtru liniar arbitrar cu kernel-ul kernel-ului la imaginea src. Rezultatul filtrării este scris în matricea dst. Dacă diafragma este în afara imaginii, pixelii de frontieră sunt completați în conformitate cu metoda specificată în borderType. Noua valoare a intensității pixelilor este calculată prin formula:
În cazul unei imagini cu mai multe canale, nucleul este aplicat fiecărui canal separat.
Următorul este un exemplu de utilizare a funcției filter2D. Programul prezentat oferă încărcarea imaginii și aplicarea filtrului liniar cu un kernel real, dat de un kernel constant. Imaginile sursă și de ieșire sunt, de asemenea, afișate.
Figura de mai jos prezintă rezultatul programului de mai sus (a se vedea figura 7.1 din dreapta). Evident, aplicarea unui filtru cu un kernel fixat în codul programului (îndrăzneț) a dus la scăderea contrastului imaginii testului original (Figura 7.1, stânga).
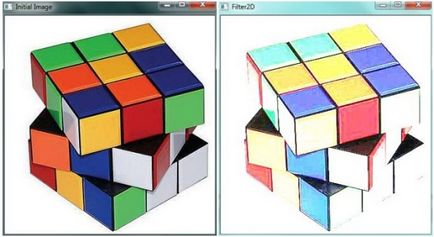
Fig. 7.1. Rezultatul aplicării filtrului
Rețineți că în cazul miezurilor mari (de ordinul a 11x11 pixeli), pentru a calcula convoluția este utilizată o transformare Fourier rapidă, în cazul micilor nuclee se utilizează un algoritm simplu. De asemenea, dacă nucleul este separabil, i. E. poate fi reprezentată ca o pereche de nuclee care pot fi aplicate secvențial rândurilor și coloanelor imaginii separat, apoi este prevăzută o implementare mai eficientă a filtrului liniar folosind funcția sepFilter2D. La apelarea acestei funcții, este necesar să se precizeze în mod explicit două kerneluri unidimensionale Kernel și columnKernel.