Conform legii gravitației universale, toate corpurile sunt atrase de Pământ cu o forță proporțională cu masa corpului (m este masa corpului și g = 9,81 m / s 2), această forță se numește greutatea corporală (gravitatea).
Când se ia în considerare echilibrul și mișcarea corpurilor de formă complexă, este important să se cunoască poziția centrului de greutate al acestui corp.
Să luăm în considerare determinarea poziției centrului de greutate al plăcii de material ABB1 A1 sub forma unui trapezoid curbilinar mărginit de curba AB. care este dată de ecuația explicită y = y (x). și de liniile x = a. x = b (a
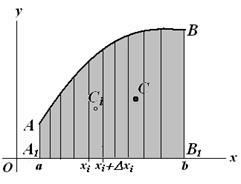
Să presupunem că densitatea de suprafață a materialului plăcii este constantă, adică cifra este omogenă. Pentru claritate, se poate presupune că greutatea specifică a materialului plăcii este 1 ( # 947; = # 961; g = 1, # 961; - densitatea materialului), atunci masa plăcii sau a oricărei părți a acesteia este măsurată de suprafața corespunzătoare.
Pentru a determina poziția centrului de greutate, împărțim placa în benzi verticale cu bazele i = 1,2, ..., n (). Centrul de greutate al fiecărei benzi este determinat de coordonate
unde u sunt coordonatele punctului curbei (= y ()).
Centrul de greutate al plăcii omogene ABB1 A1 a fost luat în considerare. ca orice alt corp, are proprietatea că poziția sa nu depinde de rotirea acestei plăci la orice unghi față de verticală. După cum se arată în cursul mecanicii teoretice, coordonatele centrului de greutate al corpului sunt date de formule
Atunci când numărul de partiții tinde spre infinit și lungimea elementelor partiției. În formulele (7.15), zona benzii i a partiției
Trecerea la limită în formulele (7.15), când și. sumele corespunzătoare sunt integrate, prin urmare coordonatele centrului de greutate al trapezului curbilinar sunt date prin formule
Note. 1. Dacă o figură plană are o axă sau un centru de simetrie, centrul de greutate al unei astfel de figuri se află pe axă sau în centrul simetriei.
2. Dacă corpul constă din părți ale căror centre de greutate sunt cunoscute, atunci centrul de greutate al figurii compozite este determinat de formulele
aici k este numărul de componente; Si și xi. yi - zona și coordonatele centrului de greutate al părții i, respectiv. Dacă figura plată are găuri, atunci centrul de greutate al acestei cifre este determinat de aceleași formule, dar zonele care corespund găurilor trebuie să fie negative.
Un exemplu. Determinați coordonatele centrului de greutate al cercului (x, y> 0). Desenați această figură plată
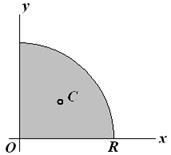
Pătrat de un sfert de cerc.
Definim integralele numărătorilor formulelor (7.16) (aceste integrale se numesc momente statice)
Astfel, coordonatele centrului de greutate al cercului triunghi sunt egale