Optimizarea este o activitate intenționată. care constă în obținerea celor mai bune rezultate în condițiile corespunzătoare.
De obicei, valoarea optimizată este legată de economia obiectului în cauză. În general, orice complex de producție poate fi considerat un obiect: un aparat, un agregat, un magazin, o fabrică, o combinație, o ramură industrială. Versiunea optimă sau cea mai bună a operațiunii obiectului trebuie măsurată printr-o măsură cantitativă - criteriul de optimitate.
Criteriul de optimitate este evaluarea cantitativă a calității optimizate. Aceasta este caracteristica principală, judecând cât de bine funcționează sistemul, funcționează acest proces, cât de bine este rezolvată problema optimizării.
Formularea problemei de optimizare poate fi diferită în funcție de scopul urmărit, în formula generală, se încheie în determinarea valorilor parametrilor de control. optimizarea indicatorului de calitate acceptat - criteriul de optimitate. care are valoarea maximă sau minimă posibilă, cu condiția respectării restricțiilor privind variabilele. impuse de cerințele tehnologice, operaționale, de proiectare, condițiile de stabilitate, capacitatea de producție, disponibilitatea materiilor prime etc.
1) probleme de optimizare statică pentru procesele care apar în regimuri staționare care rezolvă problemele de creare și implementare a unui model de proces optim;
2) problema de optimizare dinamică sau creare sarcină și implementarea controlului procesului optim în condiții de funcționare tranzitorii, sistemul de soluții care necesită un studiu al dinamicii procesului (de exemplu, start-up proces sau se transferă de la un mod la altul cu deviere minimă a calității produsului, proces discontinuu control optim ).
Pentru a rezolva problemele de optimizare, este necesar:
1. Creați un model matematic al obiectului de optimizare;
2. Selectați criteriul de optimitate și formați funcția obiectiv (funcția obiectiv poate fi nelimitată sau cu restricții asupra valorilor parametrilor individuali);
3. Definirea parametrilor de control și a posibilelor lor limitări;
4. Selectați și implementați o metodă de optimizare care ne va permite să găsim valorile extreme ale cantităților necunoscute.
Procedura de rezolvare a problemei optimizării procesului implică stabilirea (sau selecția) parametrilor de control (factori) și numărul acestora. posibilitatea schimbării care vă permite să gestionați și să optimizați procesul (acesta poate fi temperatura, presiunea, timpul, compoziția amestecului inițial etc.).
Parametrii rămași nu sunt reglați, deși valorile lor sunt luate în considerare la determinarea condițiilor optime.
Odată ce parametrii de control sunt definiți. în majoritatea problemelor de optimizare, există restricții privind intervalul acestor parametri (variabile).
Limitări - cantitățile tehnologice care, în procesul de funcționare a unității (aparatului) nu trebuie să lase toleranțele prescrise de tehnologie.
Alocați restricții privind tipul de egalități și tipul de inegalități. Limitările tipului de egalitate stabilesc o anumită valoare a unuia sau a altui parametru
Parametrul hi poate fi considerat ca fiind unul dintre intrările nereglementate controlate (compoziția materiei prime, dimensiunile dispozitivului etc.)
Limitările tipului de inegalități definesc limitele în care parametrii procesului X pot fi modificați
Toate metodele de rezolvare a problemelor optime sunt împărțite în următoarele grupuri principale.
1. Metode analitice. Ele sunt folosite atunci când putem diferenția funcția obiectivă și găsim extremumul său.
2. Metode de programare matematică (liniară, dinamică, neliniară). Pentru utilizarea acestora trebuie să calculabila funcție obiectiv: să fie algoritm cunoscut care vă permite să calculeze valoarea criteriului optimalităii pentru valori date ale factorilor.
3. Metode de căutare aleatorie (optimizare experimentală). Aplicabil dacă formularul funcției obiective nu este cunoscut. Apoi planifică și implementează experimentul în așa fel încât să obțină rezultatul optim al regiunii.
Sunt cunoscute și metode combinate care combină anumite avantaje ale metodelor individuale din diferite grupuri.
Căutarea optimă prin metode numerice. Esența metodelor numerice: un număr de valori ale F sunt calculate pentru diferite valori ale argumentelor; comparația acestor valori arată în ce direcție este necesar să se miște în spațiul factorilor pentru a se apropia de cel optim.
1. Se aplică optimizarea prin forță brută dacă numărul de opțiuni posibile este finit. Calculați funcția obiectivă pentru toate variantele posibile și selectați cea mai mare (sau cea mai mică) valoare.
2. Scanarea este o metodă apropiată forței brute, dar aplicată funcțiilor continue.
Luați în considerare, de exemplu, o scanare unidimensională - cazul când căutăm un maxim de funcție obiectivă dintr-un singur factor (căutarea unui minim este efectuată exact în același mod).
Definim limitele modificării factorului x de la a la b. Aici a și b sunt constrângeri care pot fi stabilite în orice problemă reală.
Acest interval [a, b], pe care se caută extrema funcției obiectiv, se numește intervalul de incertitudine. Problema găsirii extremumului se reduce la o reducere a intervalului de incertitudine. Metoda de scanare este rezolvată după cum urmează (Figura 1):
Alegeți un număr întreg q - numărul de valori ale funcției obiectiv, care va trebui să fie calculat. Calculați intervalul # 916; x
Amânăm intervalele de la punctul a la punctul b # 916; x (Figura 1). Limitele fiecărui interval sunt numite noduri; în figura 1 fiecare nod este indicat printr-o cruce.
a, b - limitele intervalului de incertitudine.
Figura 1 - Programul de scanare a funcției de scanare:
În fiecare nod, calculăm F (x) (vezi punctele din figura 1). Acum luați drept maxim cea mai mare dintre valorile obținute - în figură acesta este al patrulea punct din stânga. Până la sfârșitul calculului, intervalul de incertitudine # 948; va fi 2 # 916; x: maximul real se poate afla fie la dreapta, fie la stânga celui mai bun punct rezultat (linii punctate în figura 1).
Formula determină eficacitatea metodei
Metode de căutări direcționate. Căile de căutare direcționale sunt mai eficiente, dar nu au versatilitatea că scanarea este diferită. Eficacitatea lor este legată de faptul că progresul în spațiul factorilor este în direcția extremei dorite. Dar direcția căutării are următoarea cerință de bază: condiția unimodală a funcției; trebuie să aibă în regiunea admisibilă numai un extremum al semnalului dorit (un maxim, dacă căutăm un maxim, un minim în caz contrar).
Când alegem o metodă de căutare extremă, se disting două cazuri principale: 1) F depinde doar de un factor, F = F (x): atunci se face o căutare unidimensională; 2) factori mai mult decât unul - căutare multidimensională. Luați în considerare metoda de căutare unidimensională (metoda dihotomiei) și metoda de coborâre tridimensională, metoda gradientului, metoda de căutare aleatorie.
Dihotomia. Ca în descrierea scanării, luați în considerare căutarea unui maxim pe [a, b], prezentat în Figura 2.
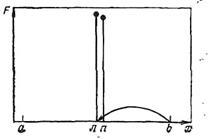
Figura 2 - Graficul căutării maxime prin metoda dihotomiei.
Împărțiți segmentul în jumătate - punctul n (stânga) din figură. Calculam valoarea F = F (n) în acest moment. Alegem o creștere mică a factorului egal cu # 949;. și a pus pe segmentul din dreapta punctul n = n + # 949; Calculăm F (n). Deoarece F (n)> F (n), așa cum se arată în figura 2, se poate argumenta că dacă F (x) este unimodală, atunci maximul este în jumătatea din stânga a segmentului.
Am abandonat jumătatea dreaptă a segmentului (nu există un maxim pe acesta). Pentru aceasta, punctul final de capăt b-este transferat la punctul n. Denumim punctul n de către b. În Figura 2 acest transfer este indicat de o săgeată. (Desigur, dacă ar exista F (n) După mutarea poziției finale a segmentului, sarcina sa întors la condițiile inițiale: se specifică un segment de la a la b, pe care este necesar să se găsească maximum. Prin urmare, se efectuează următorul ciclu de calcul, care nu diferă de cel precedent, cu excepția valorii b. Un astfel de algoritm (calculul este compus din cicluri identice, care diferă numai în condițiile inițiale) se numește iterativ. Opriți iterațiile atunci când intervalul de incertitudine este mai mic decât # 949; : Eficacitatea algoritmului de dihotomie este definită după cum urmează: fiecare pereche de calcule (punctele n și n) reduce jumătatea intervalului [a, b]. Indicăm segmentul inițial cu indexul exp. Dacă facem calcule q (q este egal), atunci Coordonați coborârea. Sunt alese coordonatele punctului de căutare inițial x1n și x2n. unitățile incrementale ale ambilor factori (pașii) H1 și H2. precum și creșteri mici ale factorilor # 949; 1 și # 949; 2. Se calculează valoarea lui F (x1n, x2n) la punctul 1 (figura 3). Mai mult, fără a schimba valoarea x2, vom începe să se miște de-a lungul axei x1, oferind la fiecare pas al acestui factor de creștere H1 (sau -H1. În funcție de timpul deplasării în ce direcție se va produce F creștere). La fiecare pas - la punctele 2, 3, 4 etc. - calculul se efectuează F. Etapele continuă până la creșterea lui F. Pașii pe care se obține valoarea mai mică a lui F nu au succes, decât pe cei anteriori; în figură sunt marcate cu cruci. După o primă etapă nereușită (punctul 6), a reveni la punctul anterior (în acest caz - la punctul 5), fixați x1 valoare și x2 încep să se schimbe, oferindu-i H2 sau -H2 increment (punctele 7, 8, 9, 10).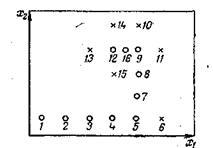
o - pași de succes; x - pași fără succes.
Figura 3. Schema de mișcare în spațiul factorilor în timpul optimizării
metoda de coborâre a coordonatelor
Apoi, din nou, se deplasează de-a lungul axei x1 (punctele 11, 12, 13), iar schimbarea de direcție (punctele 14, 15) etc. Figura 3 ilustrează o situație în care de la punctul 12 pentru a muta nicăieri: .. În toate punctele din jur (9, 13 , 14, 15), valoarea lui F este mai mică decât în cazul lui. Aceasta înseamnă că am abordat deja maximul, iar pașii majori anteriori de la punctul 12 ne conduc prin acesta. Prin urmare, reducem pașii (de exemplu, duble - vedeți punctul 16) și continuați căutarea cu pași redus. Reducerea treptei poate fi făcută în mod repetat. Dar în momentul în care pașii redusi sunt mai puțin decât respectiv # 949; 1 și # 949; 2. cred că maximul este fixat destul de precis și puteți termina calculul luând cel mai bun punct pentru optim.
Metoda de gradient există într-un număr mare de variante. Luați în considerare una dintre cele mai simple.
Alegem coordonatele punctului inițial x1n și x2n. pașii H1 și H2 și incrementări mici # 949; 1 și # 949; 2. Nu vom porni mișcarea la optim pe orice axă de coordonate, ci în direcția gradientului funcției obiectiv (sau, dacă căutăm un minim, apoi în direcția opusă gradientului). Deoarece H1 și H2 sunt luate ca incremente de coordonate, formula de gradient devine:
Pentru a calcula direcția gradientului, este necesar să cunoaștem derivații parțiali ai funcției obiective prin factori. Pentru a calcula derivatele, se efectuează o serie de calcule auxiliare (Figura 4).