Calculul Gentzen al producției naturale

§ 1. Calculul nj.

Definiția 2.1.NJ - Rezultatul constă în formule aranjate sub formă de copac.

Determinarea 2.2.Dopuscheniya - (. În acest caz, această formulă originală este „deasupra“ fundul formula H-forma concluzie) formula brută este de ieșire, fiecare ieșire care este furnizat într-o potrivire exact un N-semn figura

Toate formulele de mai jos această ipoteză și simultan deasupra formulei inferioare a acelei figuri H a concluziei la care se compară această ipoteză, precum și ipoteza însăși, se numesc dependente de această ipoteză. Astfel, concluzia face ca declarația rezultată să fie independentă de ipoteza comparată cu ea.

În conformitate cu ceea ce sa spus, formula finală de derivare nu depinde de ipoteze.

Scheme de cifre de închisoare

Introducerea conjuncției: eliminarea conjuncției:

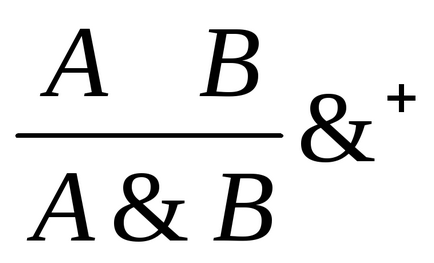
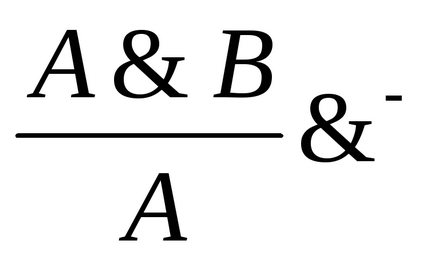
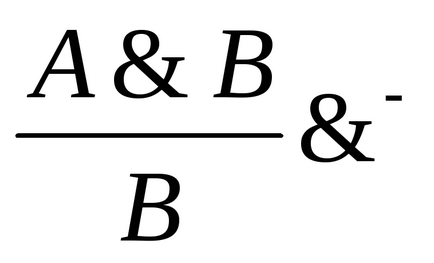
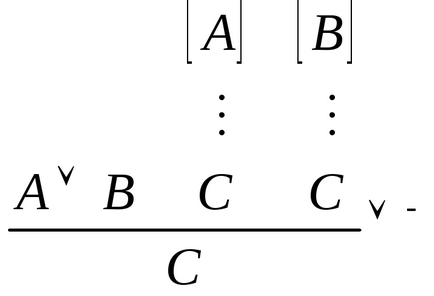
Introducerea disjuncției: Înlăturarea disjuncției:

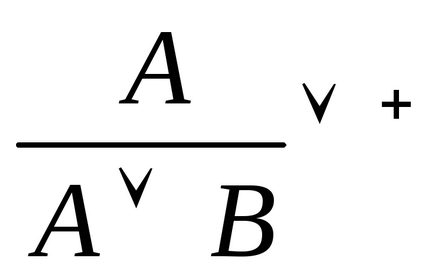
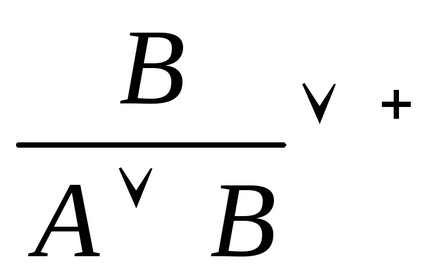
Introducerea implicării: eliminarea implicațiilor:

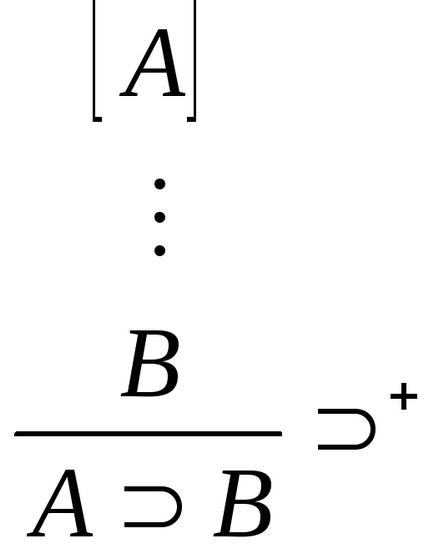
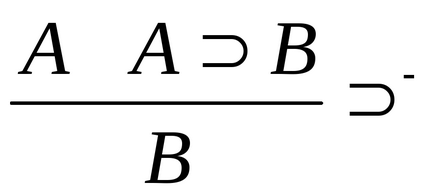
Introducerea negării: Ștergerea negării:

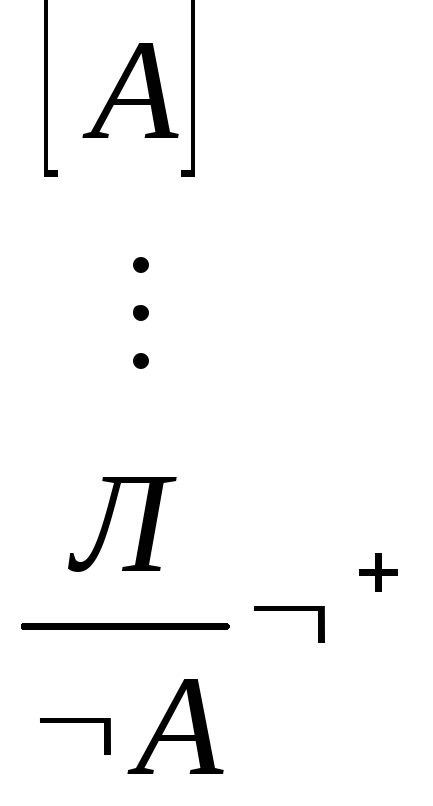
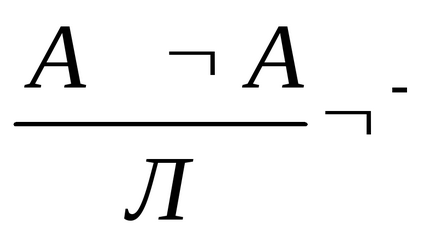
Introducerea unei declarații arbitrare:

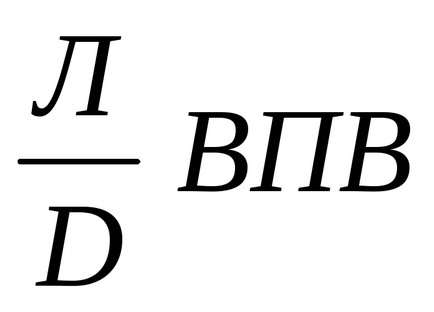
Introducerea cuantificatorului universalității: eliminarea cuantificatorului universal:

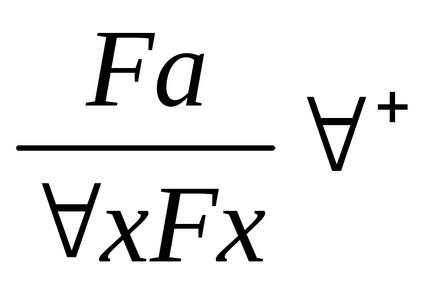
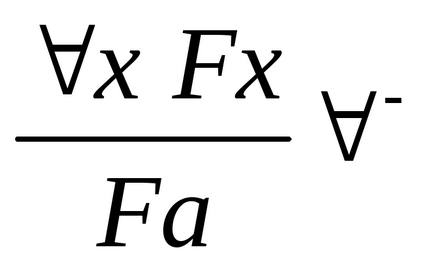
Introducerea cuantificatorului existenței: Înlăturarea cuantificatorului existențial:

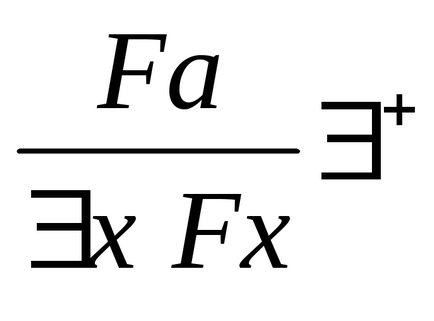
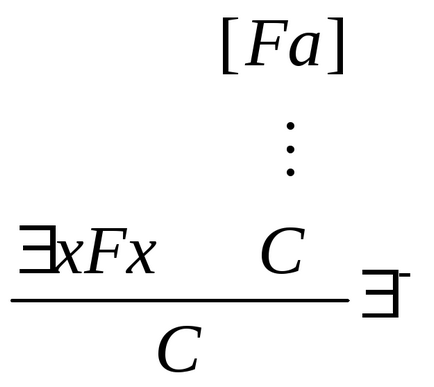
Variabila proprie a unei anumite cifre de închisoare

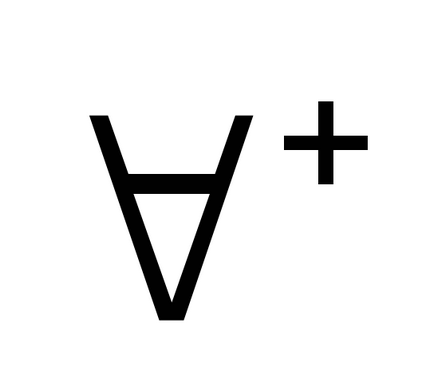
Restricționarea variabilelor:

Ieșirea NJ trebuie să îndeplinească următoarele condiții:

intrinsecă variabilă

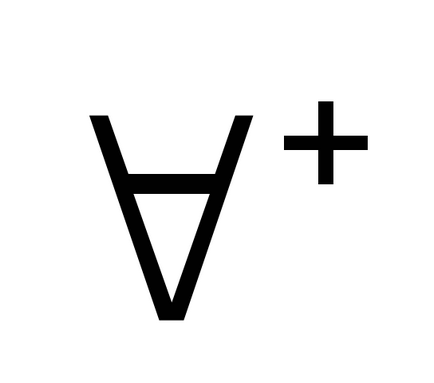
intrinsecă variabilă

Explicații la diagramele figurilor de detenție și

Semnificația ni-cifrelor concluziei.

Potrivit lui Gentzen, ideea de bază de a crea un calcul natural este legată de intenția "de a construi un astfel de formalism care să fie cât mai aproape de raționamentul folosit în realitate".

Gentzen credea că principala caracteristică care distinge calcul natural din alte, în special axiomatica, este faptul că „concluzii naturale veni nici un axiome logice, și din ipotezele din care sunt făcute concluzia logică. Și apoi rezultatul se face de unele concluzii suplimentare deja independent de ipoteze ".

Rețineți că în lista noastră de cifre schematice a concluziei, semnele din parantezele pătrate au următorul înțeles: formule oficiale formale de acest tip în orice număr (inclusiv cele zero) pot fi comparate cu figura finală ca ipoteze. Ei, prin urmare, ar trebui să fie formula originală și de ieșire să fie în firele de ieșire, care aparține corespunzător figura superioară formula concluzia (de exemplu, că formula superioară, peste care în schemă sunt parantezele pătrate, ea trebuie să fie admis).

Corespondența menționată în derivarea dintre figura H dată a concluziei și concluziile corelate cu aceasta se notează, de exemplu, prin intermediul unei numerotări generale.

Acum vom explica semnificația schemelor schematice ale concluziilor și, astfel, vom încerca să arătăm că calculul NI reproduce "raționamentul real".

+. În cuvinte, această concluzie poate fi exprimată după cum urmează: "Dacă există două declarațiiA și IV, atunci există o declarație complexă (A B)".

-. Dacă se dovedește (deține) propoziția A  B. atunci există o zicală A. sau există o vorbă. Acest fapt se reflectă în prezența a două scheme de detenție.

 +. Dacă se dovedește o propoziție A sau o propoziție. atunci există și o zicală (A B), acest fapt fiind reflectat și de prezența a două scheme de detenție.

 - (analiza cazului): Dacă este demonstrată (A B), atunci este posibilă efectuarea analizei dovezilor. Să presupunem mai întâi că A este deținut. și din aceasta deducem. Dacă mai departe de pedeapsa cu privire la ceea ce deține. din nou eliminat. tC deține, în general, chiar independent de ambele ipoteze.

 +. Dacă B este dovedit folosind Assumption A. atunci (fără această ipoteză, A urmează V, adică (A  B)).

 -. Această regulă este deja cunoscută modus ponens. Dacă A este dovedit și A  B este dovedit. apoi uB are loc.

 +. Dacă o falsă (A) rezultă din ipoteza A, atunci A nu este adevărată; are un loc.

 -: A și A înseamnă "contradicție" și nu poate corespunde realității (legea contradicției). Acest lucru este reflectat formal în cifra de concluzie

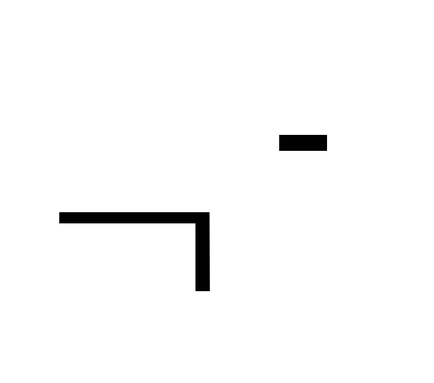
ERW: Dacă există ceva fals, atunci există vreo vorbă.

 +. Dacă F este dovedit pentru orice "pentru un arbitrar a", atunci există un "x Fx. Presupunerea că "absolut arbitrar" poate fi exprimată cu mai multă precizie după cum urmează: Fa nu depinde de nicio ipoteză în care variază subiectul.

 -. Această regulă este destul de evidentă. Dacă se dovedește că Fx este valabil pentru fiecare clasă. atunci pentru un arbitru ales din această clasă este de asemenea adevărat că Fx

 +. Dacă Fa este dovedită "pentru un arbitrar a", atunci putem afirma că există un "astfel încât Fx;

 -. Avem x Fx. Mai departe argumentăm după cum urmează: să fie exact un astfel de obiect pentru care are loc F. și anume să presupunem că este Fa. (În kachestvea necesar să se ia o astfel de variabilă, care nu este inclus vxFx. În cazul în care pe baza acestei ipoteze, vom dovedi niște vyskazyvanieS. Soderzhita care nu este și nu depinde de alte ipoteze, soderzhaschiha. CBT a demonstrat în mod independent de dopuscheniyaFa.

Denumirile introduse ale cifrelor individuale ale concluziei arată că există o sistematizare remarcabilă a acestora. Cu fiecare dintre semnele logice , , , , ,  este conectată o figură de "introducere" și o figură de "eliminare" ca semn extern al formulei. Prezența a două figuri de închisoare - și + + este o abatere pur neglijabilă, care este doar nesemnificativă. Introducerile sunt, ca să spunem așa, "definițiile" semnelor corespunzătoare, audițiile sunt doar consecințele acestor definiții. Acest lucru poate fi exprimat după cum urmează: atunci când ștergeți un anumit semn, formula la care se aplică acest lucru și semnul în cauză pot fi utilizate numai în sensul în care primesc acest semn.

Următoarele exemple ar putea clarifica ceea ce sa spus: formula A  B poate fi introdusă dacă există o derivare B din presupunerea A. Aplicând îndepărtarea la această formulă, atunci acționăm exact în același mod ca și dacă B ar rezulta din experiența deja dovedită A. Acest lucru rezultă din faptul că A  B înregistrează existența deducerii din A. Aceasta poate fi reprezentată prin următoarea schemă:

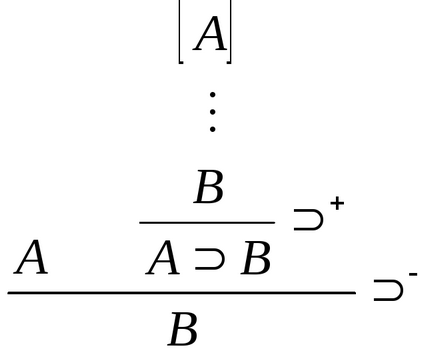
Exemplu de conjuncție:

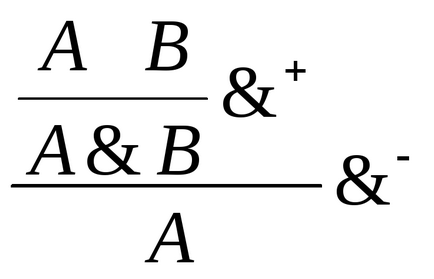
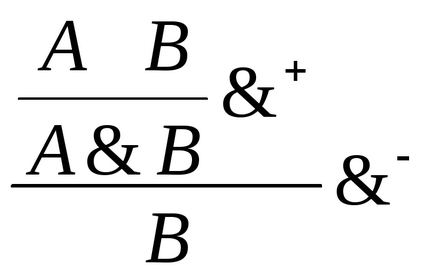
Formulele inițiale A și B se obțin în două etape, ca urmare a aplicării coerente a regulilor + și -.

Din această sistematizare a figurilor de închisoare există o negare. Cu toate acestea, negarea poate fi exclusă din calculul nostru dacă luăm în considerare A ca abreviere pentru A  A. Acest lucru este permis, deoarece dacă în unele NJ-derivație distrugem toate semnele - înlocuind fiecare formulă a formulei A cu formula A  A. se va întoarce NJ-ieșire (în această figură zaklyucheniya + i - devenit sluchayami privat i + -), și invers: dacă într-o NJ-ieșire kazhdoeA L înlocui naA. atunci vom obține din nou o derivare NJ.

Schema de cifre pentru încheierea ERW ocupă un loc special în cadrul schemelor, nu se referă la semnul logic, ci la semnul declarației.