Calcularea cojilor cilindrice se efectuează în conformitate cu GOST 14249-89 [1].
D = 1300 mm - diametrul interior al carcasei cilindrice;
L = 4500 mm - lungimea cochiliei;
p = 0,65 MPa - suprapresiune admisibilă;
pH = 0,1 MPa - presiune externă;
t = 400 # 63; C - temperatura mediului de lucru în aparat;
Oțel 12XM GOST 1050-74 (Tabelul 3.1 [2]) - materialul aparatului;
DSHT.OB. = 300 mm - diametrul sudat în carcasă;
DSHT.DN. = 125 mm - diametrul sudat în partea de jos.
CALCULAREA CAZULUI ÎNCĂRCAT ÎN INTERIORUL PRESIUNII
Grosimea peretelui este determinată de formulele:
unde S este grosimea efectivă a peretelui, mm;
Sp - grosimea peretelui calculată, mm;
p - suprapresiune internă admisibilă, MPa;
D - diametrul interior al carcasei cilindrice, mm;
[y] = 132 MPa - tensiune admisibilă, fila. 5 [1];
CR = 0,9 - coeficient de prochnostistykovogo sudură disponibile pentru sudarea numai pe o parte și cu o căptușeală de metal de sudura din rădăcină adiacente întreaga lungime a cusăturii de pe metalul de bază, Tabelul 20 [1];
Valoarea totală a creșterii:
unde C1 - o creștere a coroziunii și eroziunii, se calculează pe baza ratei de coroziune și a duratei de funcționare a dispozitivului;
C2 - o creștere a deviației minus-limită a grosimii plăcii;
C3 - creșterea tehnologică, ținând cont de reducerea grosimii foii, prin desen, ștanțare și îndoire.
Să presupunem, С1 = 2 mm, С2 = 0,3 mm, С3 = 0, apoi C, conform formulei (2) este egal cu
Să găsim grosimea efectivă a peretelui S, conform formulelor (1):
CALCULAREA CAZULUI ÎNCĂRCAT PRIN PRESIUNEA EXTERNĂ SAU OPERAȚIUNI SUB VACUU
În acest caz, grosimea peretelui cochiliei se calculează din starea de rezistență și stabilitate:
unde pH-ul este presiunea externă, MPa;
K2 = f (K1; K3) este coeficientul determinat de caracteristici. 5 [1].
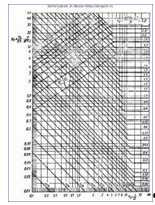
Coeficienții K1 și K3 sunt determinați prin formulele:
unde l = L + 2 * l3 - lungimea calculată a bucșei (l3 = H / 3 = D / 6, lungimea elementului adiacent, mm) mm;
nú = 2,4 - factor de stabilitate pentru condițiile de funcționare, punctul 1.4.12 [1];
E = 1,78 * 10 5 MPa - modul de elasticitate longitudinală, tab. 19 [1].
Să găsim coeficienții K1 și K3 conform formulelor (4), apoi definim coeficientul K2:
Grosimea peretelui conform formulelor (3):
Alegem max, adică Sp = 6,5 mm
Grosimea efectivă a peretelui este S # 63, 6,5 + 2,3 = 8,8 mm
Luăm S = 9 mm.
CALCULAREA SUPORTULUI CU RINGE RIGIDE ÎNCĂRCATE DE PRESIUNE EXTERNĂ
Luăm numărul de inele de rigiditate egale cu 3. le aranjăm uniform pe coajă. Apoi, distanța l1 între două inele de rigidizare de-a lungul axelor care trec prin centrul de greutate al secțiunii transversale a inelelor de rigidizare este 11 = 1125 mm.
Determinăm grosimea efectivă a peretelui cu inele de rigiditate, conform punctului 2, presupunând că l = l1:
Alegem max, adică Sp = 7,15 mm
Grosimea efectivă a peretelui este S # 63, 6,3 + 2,3 = 8,6 mm
Luăm S = 9 mm.
Parametrii parametri ai carcasei armate:
Lungimea efectivă a peretelui coajelor, mm
unde t este lățimea secțiunii transversale a inelului de rigidizare, mm.
Lățimea inelului este considerată egală cu două grosimi ale peretelui, adică t = 2S = 18mm. Atunci le este egal cu:
Alegeți min, adică le = 120,66 mm.
Moment efectiv de inerție a inelului transversal de rigiditate calculat, mm 4
unde IK este momentul de inerție a secțiunii transversale a inelului de rigiditate în raport cu axa care trece prin centrul de greutate al secțiunii transversale a inelului, mm 4;
AK - aria secțiunii transversale a inelului de rigiditate, mm 2;
e distanța dintre centrul de greutate al secțiunii transversale a inelului de rigidizare și suprafața mijlocie a carcasei, mm.
Momentul IK de inerție poate fi găsit din formula:
unde h2 este înălțimea secțiunii inelului de rigiditate, mm. Luăm valoarea lui h2 puțin mai mult decât le, adică h2 = 121 mm. atunci
Zona AK se găsește după formula:
AK = 121 * 18 = 2178 mm 2
Distanța e de formula:
Momentul efectiv al inerției I:
Momentul efectiv calculat al inerției inelului de rigiditate:
unde K5 = 0,015 - coeficient determinat de caracteristici. 11 [1].
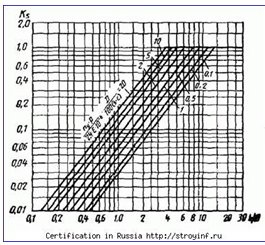
Condiția I # 63; IP este satisfăcută.
OBSHELELE ÎNCĂRCĂTOARE DE EFORT DE AJUTOR AXIAL
Grosimea peretelui trebuie calculată prin formula
Forța axială de tracțiune admisă trebuie calculată din formula
OBSHELELE ÎNCĂRCATE DE EFORT DE COMPRESIE AXIALĂ
Forța de compresiune axială admisă trebuie calculată din formula
unde forța de compresiune axială admisă [F] n din starea de rezistență
și forța de compresiune axială admisă în domeniul elastic [F] E din starea de stabilitate
În formula (23), forța de compresiune axială admisă [F] E1. sunt determinate din starea locală de stabilitate în intervalul de elasticitate al formulei
Apoi vom lua B1 = 1
și forța de compresiune axială admisă [F] E2 - de la starea de stabilitate generală d la intervalul elastic conform formulei
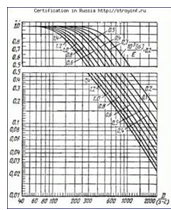
flexibilitate # 63; sunt determinate de formula
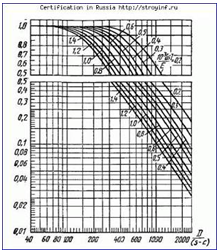
Lungimea calculată calculată lpr este luată în conformitate cu graficul 7
Notă. În cazul în care <10, формула (23) принимает вид
Pentru condițiile de funcționare (nu = 2.4), forța de compresiune admisibilă poate fi determinată din formula
coeficienţii # 63; 1 și 2 ar trebui să fie determinată de diavol. 8 și 9.
BOMELES, MOMENT DE BENDING ÎNCĂRCAT
Momentul de îndoire admisibil trebuie calculat prin formula
unde momentul de îndoire [M] n admis este calculat din condiția de rezistență prin formula
și momentul de încovoiere admisibil [M] E din starea de stabilitate din intervalul elastic conform formulei
Pentru condițiile de funcționare (n = 2.4), momentul de îndoire admisibil poate fi determinat prin formula
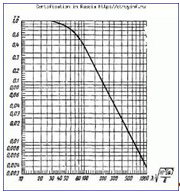
factor # 63; 3 ar trebui să fie determinată de linie. 10.
OBSHELS, ÎNCĂRCAT CU EFORTURI CROSS
Forța laterală permisă [Q] trebuie calculată din formula
unde forța laterală admisă [Q] n din condiția de rezistență
și forța transversală admisibilă [Q] E din starea de stabilitate din domeniul elastic
SHELL care funcționează în cadrul acțiunilor comune ale presiunii externe, forța axială de compresiune, momente de încovoiere și forțele laterale
Cojile care lucrează sub acțiunea comună a sarcinii sunt testate pentru stabilitate prin formula
unde [p] este presiunea externă admisă în conformitate cu punctul 2.3.2;
[F] - forță de compresiune axială impusă în conformitate cu punctul 2.3.4;
[M] este momentul de îndoire admisibil în conformitate cu punctul 2.3.5;
[Q] - forța laterală admisă conform 2.3.6