Materiale pentru prelegerea №2
Conceptul de rezoluție și mărire a microscopului
Mărirea totală a microscopului este determinată de produsul de mărire a obiectivului Mob și a ocularului (sau proiectiv) Mok:
Limita de mărire utilă a microscopului este limitată de cea mai importantă caracteristică sale - rezoluție, care este înțeleasă ca abilitatea de a primi o separat, non-drenabil detalii imagine a obiectului observat, la o anumită distanță unul față de celălalt.
Distanța minimă la care aceste detalii sunt percepute separat se numește distanța maximă admisă d. reprezentând caracteristica numerică a puterii de rezolvare a microscopului. Cu cât valoarea d este mai mică. cu cât aparatul este mai "ascuțit", cu atât mai multe detalii pe care le are în structura observată, cu cât are mai multă putere de rezolvare.
Este util să se limiteze creșterea microscopului în care structura de imagine au elemente de interes vor fi amplasate nu mai aproape decât limita distanța rezolvabilă dg ochiul observatorului.
Unde este rezoluția microscopului.
Dacă presupunem că 0,2-0,3 mm, atunci cu rezoluția microscopului de lumină 0,2 μm, creșterea, determinată prin formula (2), se ridică la 1000-1500. În principiu, puteți obține o creștere mai mare, dar nu veți putea vedea noi detalii ale obiectului, deoarece microscopul în sine nu le poate rezolva.
Astfel, principala caracteristică a unui microscop este puterea sa de rezolvare, iar creșterea lui este o caracteristică derivată, limita superioară a căreia este determinată de rezoluția conform formulei (2).
Fig. 1. Difracția de undă a luminii pe marginea diafragmei (a) și datorită distribuției sale de intensitate pe imaginea iluminată a punctului obiect (b) (prezentat schematic).
Rezoluție limitată a microscopului
Rezoluția limitată a microscopului se datorează naturii undelor luminoase și fenomenului asociat de difracție a undelor luminoase.
Dacă în calea undei luminoase există un obstacol în calea unui ecran opac, atunci o parte a undei, întârziată de obstacol, încetează să funcționeze și se formează o umbră. Totuși, în acest caz, apare un fenomen specific de învelire a unui obstacol printr-o undă, numită difracție. Ca rezultat al marginilor de deschidere a unei direcții deviere de propagare a fasciculului de lumină din original și extinderea fasciculului unghiular asociat, ceea ce duce la pătare delimitare umbră (fig. 1) și, prin urmare, la apariția de nepotrivire între subiect și imaginea sa umbra.
Nu toate razele luminoase provenind de la obiect ajung la obiectivul microscopului, deoarece unele dintre ele sunt decupate fie de diafragme, fie de montura lentilelor. Aceasta duce la difracția de la marginile diafragmelor. În acest caz, imaginea punctului O va avea forma unui cerc, intensitatea în care scade de la centru la margine și care este înconjurat de inele alternative și întunecate. Cu cat diametrul lentilei este mai mic, cu atat fenomenul de difractie este mai puternic la marginea gaurii.
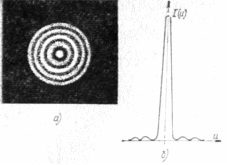
Fig. 2 Modelul de difracție al diafragmei (a) și distribuția intensității luminii (b) la macara.
Energia luminii din imaginea punctului este distribuită neuniform. Pentru prima dată, distribuția iluminării în inele de difracție a fost investigată de cercetătorul englez Airy (1811-1892), iar cercul central al punctului de difracție a fost denumit cercul Airy. Cea mai mare parte a energiei luminoase a imaginii este concentrată în cana Airy (aproximativ 84%) și primele două sau trei inele (Figura 2).
Calcularea distribuirii iluminării în inele de difracție reduce la determinarea rădăcinilor funcției Bessel J1 (α). Argumentul funcției Bessel în acest caz este o cantitate proporțională cu diametrul diafragmei
b este diametrul diafragmei,
Legea variației intensității luminii I din imaginea de difracție este descrisă apoi ca
Raza inelelor de difracție care corespund consecutiv maximelor și minimelor de iluminare (intensitate) sunt calculate din formula
- un anumit coeficient numeric, exprimându-se în "unități optice", ale căror valori sunt prezentate în tabelul 1.
k este numărul inelului (ușor sau întunecat);
a0 este unghiul de ieșire al fasciculului difracționat din diafragma din spațiul imaginii (unghiul de deschidere).
n este indicele de refracție
Valorile coeficienților obținuți ca rezultat al calculelor sunt prezentate mai jos:
Tabelul 1 Valorile coeficienților zk,
După cum rezultă din datele date, coeficientul pentru primul inel închis este de 3,83. Înlocuind această valoare în formula (5) și luând, ajungem ca raza primului inel întunecat din modelul de difracție observat în planul focal al obiectivului,
Astfel, raza cercului central, cel mai intens, numită cerc aerian sau cerc împrăștiat, este calculată ca
n este indicele de refracție pentru spațiul dintre obiect și obiectiv;
M - mărirea lentilei;
Pe măsură ce unghiul orificiului sau diametrul diafragmei scade, dimensiunea imaginii rezultate va fi din ce în ce mai diferită de cea ideală.
Apariția pe o imagine distorsionată a unui cerc în loc de un punct este echivalentă cu imaginea unui obiectiv obiectiv ideal sub forma unui cerc cu o rază
Această valoare este considerată distanța maximă permisă a dispozitivului optic (când se ia în considerare numai eroarea de difracție luată în considerare aici).
Partea vizibilă a spectrului este limitat la o regiune îngustă de lungimi de undă de 0,4 până la 0,8 microni, crescând astfel puterea de rezoluție (și cu ea creșterea benefică) în microscopie optică se realizează prin utilizarea de fluid imersiune special cu un indice de refracție. Magnitudinea un unghi de deschidere de lentile de înaltă calitate este de aproximativ (sinα0 ≈0,9), astfel încât valoarea maximă este obținută la distanță rezolvabile aproximativ egală cu jumătate din lungimea de undă a luminii folosite, T. E. 0,2 microni.
Aplicarea razelor ultraviolete cu lungimea de undă de 0,2 până la 0,25 microni dând aproximativ îmbunătăți de două ori puterea de rezoluție, dar în acest caz au existat dificultăți legate de necesitatea de fabricație transparent optic la materiale ultraviolete lângă cu absorbție UV puternic în obiect și focalizarea de complexitate.
Folosirea radiației cu raze X scurt (λ ~ 0,2 nm) nu este posibilă, deoarece razele X este aproape nu refractată și, prin urmare, nici materiale pentru producerea optică corespunzătoare.
Rezolvarea sistemului optic
Dacă razele dintr-o sursă de lumină punctuală trec printr-un sistem optic real (lentilă, lentilă etc.), atunci în planul focal al sistemului se formează un model de interferență sub forma unui cerc aeros. Dacă folosim o sursă de lumină extinsă, atunci când razele trec prin sistemul optic, fiecare punct al sursei va da cercul său, ca urmare a formării unui model complex de interferență în planul imaginii sistemului.
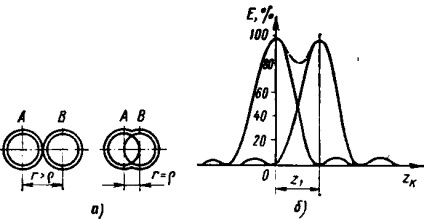
Fig. 3 Cu privire la conceptul de putere de rezolvare a unui sistem optic:
- poziția imaginilor de interferență ale punctelor A și B în funcție de rezoluția acestora;
- graficul distribuției intensității în imaginea a două puncte luminoase
În cazul în care două puncte luminoase reprezentate de un sistem optic se află la distanțe foarte mici unul față de celălalt, modelele de difracție de împrăștiere pot fi parțial suprapuse sau îmbinate într-una. Dacă într-o imagine atât de complexă sistemul optic ne permite să observăm separat două puncte distanțate, atunci ele spun că sistemul "rezolvă" aceste puncte.
Dacă distanța dintre centrele punctelor de difracție ale imaginilor A și B r denota (. Figura 3a), aceste puncte vor fi văzute separat, cu condiția ca, în cazul în care - raza primului minim (sau Airy cerc).
Distanța minimă limită dintre două puncte la care aceste puncte poate fi observată separat se numește rezoluție sau limită de rezoluție a sistemului optic.
De obicei, atunci când se evaluează sistemele energetice de dizolvare utilizat criteriul Rayleigh conform căruia trebuie furnizate cazul limită, atunci când imaginile din cele două spoturi luminoase sunt văzute separat. Maximul maxim de difracție al unuia dintre puncte coincide cu primul minim al celui de-al doilea punct. Dacă, imaginile de difracție ale punctelor se îmbină, atunci ei spun că sistemul "nu rezolvă astfel de puncte".
Puterea de rezolvare este determinată într-o măsură liniară sau unghiulară.
pentru lentile fotografice - numărul de linii (sau lovituri) pe milimetru,
pentru obiectivele microscopice - în micrometre.
Rezoluția teoretică a unui sistem optic ideal conform criteriului Rayleigh poate fi determinată liniar prin formula (8) pentru.
Curba de intensitate rezultată, observând două puncte, va avea două maxime și o scădere a iluminării între ele - un minim (Fig.3, b). În Fig. 3b, valoarea relativă a intensității iluminării E în procente este reprezentată de-a lungul axei de coordonate și argumentul funcției Bessel care descrie distribuția luminii în imaginea de difracție a punctelor luminoase este reprezentat de-a lungul axei abscise.
Se crede că ochiul distinge acest minim, cu condiția ca iluminarea în el să nu fie mai mare de 80% din iluminarea din oricare dintre cele maxime. Astfel, ochiul va distinge în mod clar ambele maxime.
Experimentele confirmă faptul că o imagine separată a două puncte sau linii poate fi observată dacă acestea sunt situate la o distanță mai apropiată de, cu condiția ca iluminarea la minimum să nu depășească maxim 74% din iluminare.