Graficul funcției de eroare
În matematică, funcția de eroare este o funcție non-elementară. apărut în teoria probabilității. statisticile și teoria ecuațiilor diferențiale parțiale. Acesta este definit ca
.
Funcție suplimentară de eroare. Denumita (desemnată uneori, este determinată prin funcția de eroare:
.
Funcție complexă de eroare. notată cu w (x). este, de asemenea, determinată prin funcția de eroare:
.
- Funcția de eroare este ciudată:
- Pentru orice complex x,
- Funcția de eroare nu poate fi reprezentată prin intermediul funcțiilor elementare. dar, extinderea expresiei integrabile într-o serie Taylor și integrarea termenului cu termen, putem obține reprezentarea sa sub forma unei serii:
Această egalitate deține (și seria converge) pentru orice real x. și pe întregul plan complex. Secvența numitorilor formează secvența A007680 în OEIS.
- Pentru calcularea iterativă a elementelor seriei, este util să o prezentăm într-o formă alternativă:
deoarece este factorul care transformă termenul i al seriei în (i + 1) -th, numărarea primului termen al lui x.
- Funcția de eroare la infinit este unitatea; Totuși, acest lucru este valabil numai când se apropie infinitul de-a lungul axei reale, deoarece:
- Când se ia în considerare funcția de eroare în planul complex, punctul va fi esențial pentru el.
- Derivatul funcției de eroare este derivat direct din definiția funcției:
- Funcția de eroare inversă este o serie de
Prin urmare, seriile pot fi reprezentate în următoarea formă (rețineți că fracțiunile sunt reduse):
[1]
Secvențele numărătorilor și numitorilor după abreviere - A092676 și A132467 în OEIS; succesiunea numărătorilor înainte de abrevierea este A002067 în OEIS.
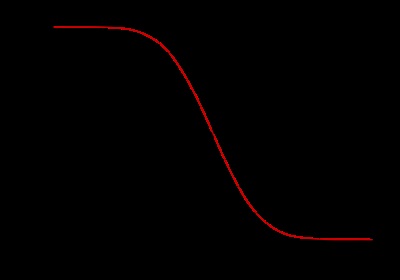
Funcție suplimentară de eroare
cerere
Dacă setul de numere aleatorii este supus unei distribuții normale cu deviația standard σ. atunci probabilitatea ca numărul să se abată de la media cu nu mai mult de a. este egal cu.
Funcția de eroare și o funcție de eroare suplimentară sunt întâlnite în rezolvarea anumitor ecuații diferențiale, de exemplu, ecuația de căldură cu condițiile limită descrise de funcția Heaviside ("pas").
În sistemele de comunicații optice digitale, probabilitatea de eroare pe bit este de asemenea exprimată printr-o formulă care utilizează funcția de eroare.
Expansiune asimptotică
Pentru x mare, este utilă o extensie asimptotică pentru funcția de eroare suplimentară:
Deși această serie se diferențiază pentru orice x finit, în practică primii câțiva termeni sunt suficienți pentru calcularea cu o precizie bună, în timp ce seria Taylor converge foarte lent.
O altă aproximare este dată de formula
Funcții înrudite
Pentru o scară și o schimbare, funcția de eroare coincide cu distribuția integrală normală. notată cu Φ (x)
Funcția inversă la Φ. cunoscută ca funcția de cuantilă normală, este denaturată și exprimată uneori prin funcția de eroare normală
Distribuția integrală integrală este mai des utilizată în teoria probabilităților și în statisticile matematice, în timp ce funcția de eroare este mai des utilizată în alte secțiuni ale matematicii.
Funcția de eroare este un caz special al funcției Mittag-Leffler. și poate fi reprezentată și ca o funcție hipergeometrică degenerată (funcția Kummer):
Funcția de eroare este, de asemenea, exprimată în termeni de integrate Fresnel. În ceea ce privește funcția gamma incompletă regularizată P și o funcție gama incompletă,
Funcții de eroare generalizate
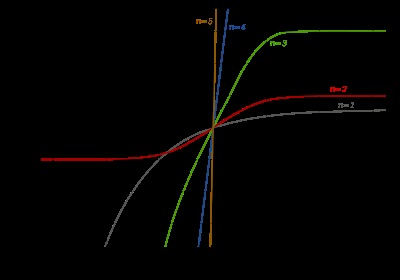
Graficul grafic al funcțiilor de eroare generalizate En (x):
linia gri:
linia roșie:
linia verde: E3 (x)
linia albastră: E4 (x)
linia galbenă: E5 (x).
Cazurile notabile sunt:
- E0 (x) este o linie dreaptă care trece prin origine:
- E2 (x) este funcția de eroare.
După împărțirea cu n. toate En cu n ciudat arata ca (dar nu identice). Toate En cu even n arata, de asemenea, similare, dar nu identice, după împărțirea cu n. Toate funcțiile de eroare obfuscate cu n> 0 arată asemănătoare cu semi-axa x> 0.
La jumătatea liniei x> 0, toate funcțiile generalizate pot fi exprimate în funcție de funcția gamma:
În consecință, putem exprima funcția de eroare prin intermediul funcției gamma:
Integrări iterate ale funcției de eroare adițională
Integalele iterative ale funcției de eroare suplimentare sunt definite ca
Ele pot fi extinse într-o serie:
din care urmează proprietățile de simetrie
punerea în aplicare
În standardele C și C ++, funcția de eroare și o funcție de eroare suplimentară nu sunt disponibile în biblioteca standard. Cu toate acestea, în GCC (GNU Compiler Collection) aceste funcții sunt implementate ca dublu erf (dublu x) și dublu erfc (dublu x). Funcțiile se găsesc în fișierele antetului math.h sau cmath. Există, de asemenea, perechi de funcții erff (), erfcf () și erfl (), erfcl (). Prima pereche primește și returnează valori de tip float. iar a doua - valori de tip double long. Funcțiile corespunzătoare sunt de asemenea conținute în biblioteca Math a proiectului Boost.
În limba [2]. Clasa Erf se află în pachetul org.apache.commons.math.special din [3]. Cu toate acestea, această bibliotecă nu este una dintre bibliotecile Java standard 6.
literatură
- Milton Abramowitz și Irene A. Stegun, ed. Manual de funcții matematice cu formule, grafice și tabele matematice. New York: Dover, 1972. (Vezi partea 7)
Link-uri externe
Urmăriți ce este "integralitatea probabilității" în alte dicționare:
PROBABILITATEA INTEGRALĂ - eroare integrală, funcție În teoria probabilității, nu se folosește I. și funcția de distribuție normală: așa-numitul. Probabilitatea gaussiană integrală. Pentru o variabilă aleatoare X având o distribuție normală cu matematică. așteptarea 0 și varianța s2, ... ... Enciclopedia matematică
Integralitatea probabilității este denumirea mai multor funcții speciale legate între ele. Integolul se numește integral probabilitatea Gaussiană. Pentru o variabilă aleatoare X care are o distribuție normală cu așteptarea matematică 0 și varianța σ2, ... ... Marea Enciclopedie Sovietică
INTEGRAL PROBABILITY - nume. mai multe. legate unul cu altul special. f. ții De exemplu. I. c. Gauss ... Mare dicționar encyclopedic politehnic
Coliziunea Integrala - coliziune expresie integrală care constituie partea dreaptă a ecuației Boltzmann, care determină rata de schimbare a funcției de densitate a particulelor din cauza coliziunilor dintre ele: Uneori coliziunea integrantă ... ... Wikipedia
INTEGRAL COLIZIUNILOR - membru în cinetic ecuația Boltzmann schimbare egală a particulelor Funcția de distribuție f (sau cvasi-particule) pe unitatea de timp în volumul fazei de celule din cauza coliziunilor între acestea; numele său. de asemenea, operatorul de coliziune. I. cu. este egal cu (... ... Enciclopedie fizică
Formularea unei integrale peste căile - formularea unei integrale peste traetoriyam a mecanicii cuantice este descrierea teoriei cuantice, care generalizează principiul mecanicii clasice. Acesta înlocuiește denumirea clasică a unei singure traiectorii, unic pentru sistemul la suma sau ... ... Wikipedia
integrantă funcțională - (cale integrală, integrală, calea Feynman integrală calea) de înregistrare sau rezultatul integrării funcționale (integrarea cale). Acesta găsește cea mai mare aplicație în fizica cuantică (teoria cuantică ... Wikipedia
- Funcții speciale și aplicațiile acestora. N. N. Lebedev. Cartea conține o expunere sistematică a bazelor teoriei celor mai importante funcții și aplicații speciale ale acestei teorii la problemele fizicii și ingineriei matematice. Considerat: gamma function, integral ... Mai multe informatii Cumpara pentru 664 UAH (only Ukraine)
- Funcții speciale și aplicațiile acestora. Manualelor. 3 ed. Cartea conține o expunere sistematică a bazelor teoriei celor mai importante funcții și aplicații speciale ale acestei teorii la problemele fizicii și ingineriei matematice. Considered: gamma function, integral ... Mai multe informații Cumpărați pentru 523 руб
- Funcții speciale și aplicațiile acestora. N. N. Lebedev. Cartea conține o expunere sistematică a bazelor teoriei celor mai importante funcții și aplicații speciale ale acestei teorii la problemele fizicii și ingineriei matematice. Considered: gamma function, integral ... Mai multe informatii Cumpara pentru 469 руб