Fluxul vectorului de intensitate a câmpului electric prin orice suprafață închisă aleasă arbitrar este proporțională cu sarcina electrică închisă în interiorul acestei suprafețe.
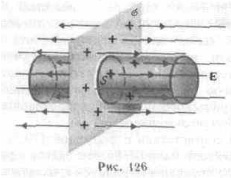
Un plan infinit este încărcat cu o densitate constantă a suprafeței (- sarcină pe unitate de suprafață).
Liniile de tensiune sunt perpendiculare pe planul examinat și sunt îndreptate departe de acesta în ambele direcții. Ca mental construi o suprafață închisă cilindru, care sunt paralele cu planul de bază încărcat, iar axa perpendiculară pe acesta. Deoarece formarea unui cilindru paralel cu liniile de tensiune (cosα = 0), intensitatea vectorului de flux prin suprafața laterală a cilindrului este egală cu zero, în timp ce fluxul total prin cilindru este egală cu suma prin firele sale de bază (baze pătrate sunt egale și En bază coincide cu E), m. e. este egal cu 2ES.
Încărcarea în interiorul suprafeței cilindrice construite este σS. Potrivit teoremei Gauss. de unde
Din formula rezultă că E este independentă de lungimea cilindrului, r. E. Intensitatea câmpului la orice distanță aceeași magnitudine, cu alte cuvinte, câmpul este încărcat uniform plan uniform.
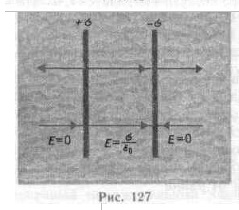
Câmpul a două planuri paralele infinite de planuri diferite
(Figura 127). Lăsați avioanele să fie încărcate cu încărcături uniform diferite, cu densități de suprafață + σ și -σ. Câmpul acestor avioane se găsește ca o suprapunere a câmpurilor create de fiecare dintre planuri separat.
În figură, săgețile superioare corespund câmpului din planul încărcat pozitiv, cele mai mici din planul negativ. În stânga și în dreapta câmpului sunt scăzute planurile (liniile de tensiune sunt direcționate unul spre celălalt), prin urmare aici intensitatea câmpului este E = 0
În regiunea dintre avioane E + + E- (E + și E sunt determinate de formula), prin urmare, tensiunea rezultată :.
Astfel, forța de câmp rezultată în regiunea dintre planuri este descrisă de această formulă, iar în afara volumului delimitat de planuri este zero.
Câmpul unei suprafețe sferice încărcate uniform.
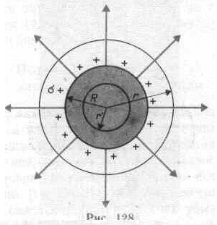
O suprafață sferică de rază R cu sarcină totală Q este încărcată uniform cu o densitate a suprafeței de +0. Datorită distribuției uniforme a sarcinii pe suprafață, câmpul creat de ea are o simetrie sferică.
Prin urmare, liniile de tensiune sunt direcționate radial. Construim mental o sferă de rază r. având un centru comun cu o sferă încărcată. Dacă r> R. atunci întreaga încărcătură Q, care creează câmpul în cauză, cade în suprafață și, prin teorema lui Gauss. de unde:
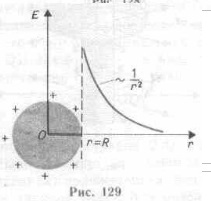
Pentru r> R, câmpul scade cu distanța r conform aceleiași legi ca și pentru o încărcare punct. O diagramă a dependenței lui E de r este prezentată în Fig. 129. Dacă r '