Viteza majorității reacțiilor dintre substanțele solide este limitată de difuzia reactivului prin stratul de produs.
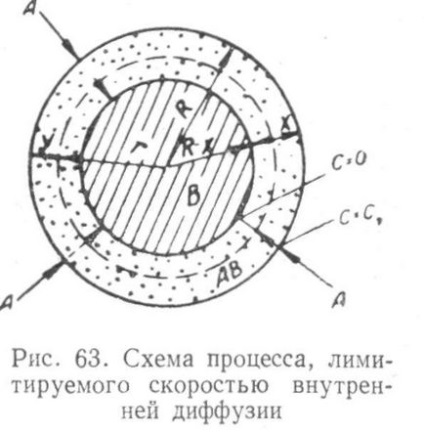
În tipul general al acestor reacții, substanța A reacționează cu substanța B, formând produsul AB (Figura 63), grosimea stratului care crește continuu în timpul procesului. In acest compus caz A (sau produsul său de descompunere) diffuses la suprafață prin stratul de substanță produsului B AB la o rată mult mai mică decât rata de reacție chimică între substanțele A și B, astfel încât difuzia determină complet cinetica procesului.
Deoarece rezistența la difuzie exterioară este mult mai mică decât rezistența la difuzie a produsului AB, concentrația substanței A în suprafața care o separă de AB este practic constantă. În suprafața care separă AB și B, concentrația substanței A este invariabil zero datorită ratei foarte ridicate (în comparație cu rata de difuzie) a interacțiunii chimice A cu B.
După cum sa arătat mai sus, Yander, pe baza cineticii tipului de reacții descrise, a pornit de la ecuația diferențială Fick pentru viteza de difuzie printr-un strat de difuzie plană. După obținerea ecuațiilor (91) și (93) în acest fel, Yander le-a extins la reacții în amestecuri sub formă de pulbere constând din particule sferice, cubice și similare "în vrac".
Este totuși evident că ecuațiile de mai sus pot fi aplicate doar particulelor sferice, cubice și similare
valori mici ale lui x / R, unde x este grosimea stratului de difuzie al produsului
AB și R este raza inițială a boabelor reactivului "acoperit", adică numai în cazul gradelor mici de conversie a substanței B în produs. În acest caz, majoritatea covârșitoare a datelor experimentale ale lui Yander aparțin.
La grade mari de conversie a substanței B și, respectiv, a valorilor mari de -x / R, ecuațiile (91) și (93) derivate pentru
Cazul "plat", de exemplu, pentru o sferă, nu este aplicabil.
În acest sens, și ca funcție derivate Yanderom utilizate pe scară largă în aplicații la o varietate de grade de conversie, era indicat să se deducă modele corespunzătoare pentru boabe sferice. Această problemă a fost rezolvată de Ginstling și Brownstein [388].
Pentru aceasta, în plus, introducem notația: C este concentrația substanței A în stratul de produs AB; C1 este concentrația lui A la interfața A-AB; D este coeficientul de difuzie A în AB;
r este distanța de la interfața A-AB la o anumită suprafață sferică arbitrară în direcția difuziei.
coeficientul de proporționalitate (unde p este specificul
greutate și p - greutate moleculară AB; n este coeficientul stoichiometric al reacției, exprimând numărul de moli ai substanței A care reacționează cu un mol C).
Din cauza simetriei sferice, concentrația C a substanței A în stratul de produs AB este o funcție numai a distanței r din centrul mingii. C (z) poate fi găsită din soluția ecuației Fick, care în cazul simetriei sferice și în coordonatele sferice are forma expresiei (32).