Soluția problemelor practice în formarea contururilor tehnice complexe întâmpină o problemă precum imposibilitatea de a reprezenta întregul contur al unei singure curbe. Aceasta a dus la necesitatea de a construi curbe compuse (curbe formate din arce simple).
În tehnică, aceste curbe sunt numite contururi, în matematică ele sunt mai bine cunoscute sub numele de spline. Principala caracteristică a conturului este netezirea. Prin netezime se înțelege numărul de derivate potrivite (ecuații de îmbinare a curbelor) la punctele de joncțiune.
Cea mai simplă variantă a construirii unei curbe compuse este din arce de cercuri.
Cercurile pot fi îmbinate astfel încât tangentele comune să fie localizate la punctele de joncțiune. O astfel de îmbinare corespunde ordinului de netezire (numai primii derivați coincid).
Pentru a construi acest contur, vom folosi ideea conjugării radius-conjugate a arcurilor circulare. Informația inițială este o serie de puncte (1, 2, 3, ..., n) și o tangentă la un capăt al acestei serii, de exemplu, t i (Figura 1).
Datorită faptului că cercul este o curbă cu trei parametri, pentru construcția sa, în plus față de punctul i, este necesar să se definească mai multe, de exemplu (i + 1) sau (i-1). Fără a încălca generalitatea argumentelor, luați în considerare varianta cu punctul (i + 1) (a se vedea figura de mai jos).
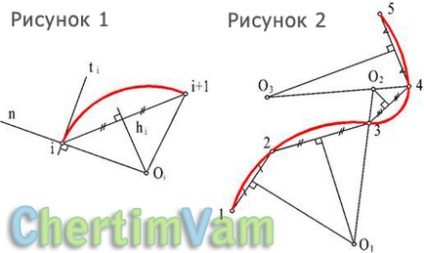
Figura 1 - Construirea unui arc de cerc cu parametri date
Figura 2 - Construirea unui contur de buna calitate
Soluția grafică este după cum urmează: prin punctul i, normalul este n. Punctele finale i și (i + 1) sunt unite printr-o coardă. O perpendiculară h este construită la mijlocul coardei. Intersecția n normală și perpendiculară h și determinarea poziției centrului cercului dorit. Raza cercului coincide cu segmentele [o-i] și [o- (i + 1)]. Tangenta la cercul construit va fi perpendiculară pe raza trasată la punctul (i + 1).
Centrele cercurilor contigue se află pe o linie care trece prin punctul de tangență. Astfel, definiția montei centrului cercului cu i-există la intersecția liniilor O i (i + 1) perpendicular pe coarda de mijloc (i + 1) (i + 2) (Figura 2).
Curbe de desenare
Mai jos este construirea celor mai frecvent utilizate curbe. Imaginea arată curba și salvează toate construcțiile. Algoritmul pentru construirea curbei este descris mai jos.
Curbe locale
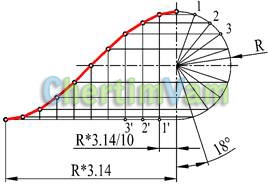
Figura 3 - Construirea unui sinusoid
Un sinusoid este o curbă plană care descrie grafic schimbarea sinusului, în funcție de argumentul său (unghiul). Pentru a construi un sinusoid, un cerc de rază R este împărțit într-un număr arbitrar de părți egale. Pe linia orizontală, compuneți un segment egal cu jumătate din lungimea cercului (R * 3.14) și împărțiți-l cu același număr de părți egale. Dintre toate aceste segmente (punctele 1 „2' , 3“) se realizează linii verticale până la intersecția cu liniile orizontale care provin de la capetele razelor respective (1,2,3 punct).
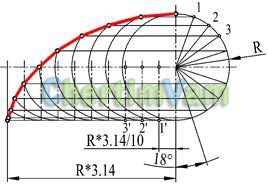
Figura 4 - Construcția cicloidului
Un cicloid este o curbă formată dintr-un punct al unui cerc de rulare fără alunecare de-a lungul unei linii drepte. Pentru a construi un cicloid, un cerc de rază R este împărțit într-un număr arbitrar de părți egale. Pe linia orizontală, compuneți un segment egal cu jumătate din lungimea cercului (R * 3.14) și împărțiți-l cu același număr de părți egale. Din capetele acestor segmente (punctele 1 ', 2', 3 ') se trasează linii verticale la intersecția cu linia centrală orizontală. Aceste puncte sunt centrele cercurilor de rază R. Intersecția cercurilor cu liniile orizontale corespunzătoare care provin de la capetele razelor (1,2,3 punct) va indica cicloidă.
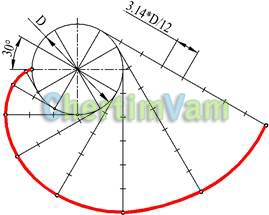
Figura 5 - Construirea unui val
Un cerc involuntar este o curbă care descrie un punct de rulare liniară fără alunecare de-a lungul unui cerc fix. Cercul de diametru D este împărțit într-un număr arbitrar de părți egale. Din punctele de divizare, sunt trase tangente la cerc, pe care sunt depuse 1, 2, 3, respectiv, respectiv. părți ale unui cerc.
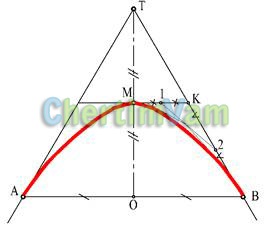
Figura 6 - Construirea unei parabole
O parabolă se numește o curbă obținută prin intersecția unui con și a unui plan paralel cu generatorul conului. Când se specifică parabola cu punctele de graniță A și B și punctul de intersecție a tangentelor T, curba este construită prin metoda divizării proporționale.
Segmentul AB este împărțit în jumătate la punctul O, segmentul OT - și în jumătate la punctul M, segmentul MC - la punctul 1, KB - la punctul 2 etc.
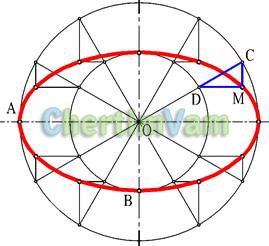
Figura 7 - Construcția unei elipse
Curba obținută la intersecția conului și planul care intersectează întregul generator al conului este eliptic.
Elipsa este mai convenabilă pentru a costa pe semi-axele sale (OA mare și OB obișnuit).
Pentru a construi o elipsă a avut loc două cerc coaxial raze OA și OB Holding, sistemul de linii arbitrare de operare și de construcție în continuare a „cheie“ (triunghi SDM cu laturile paralele cu axele elipsei) pentru a determina poziția punctului curent al elipsei M.
Construcții geometrice
Mai jos sunt prezentate cele mai comune tipuri de construcții geometrice și este descris un algoritm de construcție.
Tangentă la o elipsă
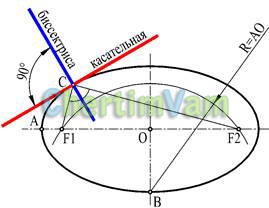
Figura 8 - Tangenta la o elipsă
Construcția tangentei la eliptică (cu semi-axe OA și OB) într-un punct predeterminat C ar trebui să înceapă cu construcția focii elipsă, F1 și F2 punctele.
Construiți un cerc centrat la punctul B și o rază egală cu semiaxul principal OA. În intersecția cercului cu axa orizontală, marcați punctele F1 și F2. Construiți bisectorul unghiului F1CF2. Linia dreaptă perpendiculară pe bisector și care trece prin punctul C va fi tangentă la elipsă la un anumit punct.
Construcția bisectorului unghiului
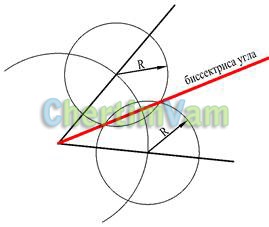
Figura 9 - Construcția bisectorului unghiular
Din vârful unghiului printr-o rază arbitrară vom construi un arc de cerc. Din punctele de intersecție a arcului de cerc cu laturi egale cu unghi circumferențial construi arbitrar rază R. Linia care trece prin vârful unghiului și punctul de intersecție a cercurilor, - unghiul bisectoarei.
Construcția geometrică a conjugării liniilor
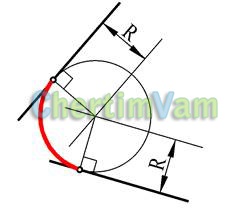
Figura 10 - Conjugarea liniilor drepte cu un cerc cu o anumită rază R
La o distanță R de la liniile date, construiți linii auxiliare paralele cu ele. Din punctul de intersecție al liniilor auxiliare, construiți un cerc conjugat cu o anumită rază R. Marcați punctele de conjugare. Ele se află pe perpendiculare trase din centrul cercului conjugat până la liniile drepte date.
Construcția conjugării unei linii drepte și a unui arc
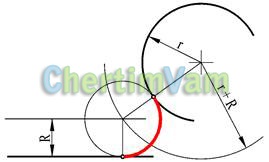
Figura 11 - Conjugarea unui cerc cu o anumită rază R a unei linii drepte și a unui arc
La o distanță R de la o linie dată, construiți o linie auxiliară paralelă cu ea. Din centrul arcului conjugat trageți un arc de cerc cu raza r + R. Din punctul de intersecție al arcului construit și al liniei auxiliare, construiți un cerc conjugat. Marcați punctele de împerechere.
Construirea conjugării a două cercuri
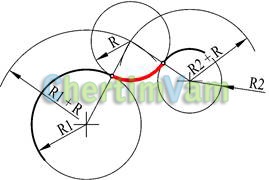
Figura 12 - Conjugarea exterioară cu un cerc cu o anumită rază R a două cercuri cu raze R1 și R2
Din centrele unor cercuri date trageți arce de cercuri auxiliare cu raze R1 + R și R2 + R. Din punctul de intersecție al arcurilor cercurilor auxiliare, construiți un cerc conjugat cu raza R. Marcați punctele de conjugare. Ele se află pe liniile care leagă centrele cercurilor.
Construcții geometrice de conjugare mixtă
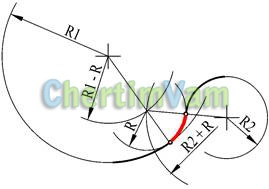
Figura 13 - Conjugarea mixtă a unui cerc cu o rază dată R a două cercuri cu raze R1 și R2
Din centrele cercurilor date trageți arce de cercuri auxiliare cu raze R1-R și R2 + R. Din punctul de intersecție al arcurilor cercurilor auxiliare, construiți un cerc conjugat cu raza R. Marcați punctele de conjugare. Ele se află pe liniile care leagă centrele cercurilor.