Prezentare pe tema: "Lungimea unui cerc este numărul la care perimetrul poligoanelor obișnuite inscripționate în acest cerc crescând numărul laturilor lor." "Teorema". - Transcriere:
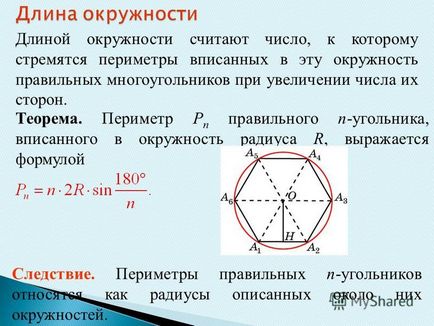
1 Lungimea unui cerc este numărul la care perimetrele poligoanelor obișnuite inscripționate în acest cerc crescând numărul lor. Teorema. Perimetrul P n al unui regulat n-gon înscris într-un cerc de rază R este exprimat prin formula COROLLARY. Perimetrele n-gonilor obișnuiți sunt considerați ca fiind razele cercurilor circumscrise în jurul lor.
2 Jumătatea circumferinței unei raze de unitate este notată cu litera greacă π. Astfel, circumferința unei raze de unitate este de 2π. Din teorema considerată mai sus rezultă că lungimea unui cerc cu raza R este 2πR. Astfel, pentru circumferința C a razei R, putem scrie următoarea formulă: C = 2πR. Teorema. Raportul dintre lungimile a două cercuri este egal cu raportul dintre razele lor.

3 Pentru un calcul aproximativ al numărului π într-un cerc unic, este înscris un poligon regulat și se găsește jumătate de perimetru. Cu cât numărul de laturi al poligonului inscripționat este mai mare, cu atât este mai precis valoarea pentru numărul π. Primul calcul al numărului π, folosind un raționament riguros, a fost făcut de cel mai mare matematician al antichității, Archimedes (BCE). În lucrarea sa "Cu privire la măsurarea unui cerc" el a demonstrat că inegalitățile dețin pentru numărul π. În practică, valoarea aproximativă a numărului π este considerată a fi 3.14.

4 Unghiurile centrale ale 1 o împart întreaga circumferință în 360 de sectoare egale. Prin urmare, lungimea arcului cercului la 1 ° face parte din lungimea întregii circumferințe, adică este egal cu. Lungimea l a unui arc cu un cerc de rază R în grade φ va fi exprimată prin formula

Egalitatea, exprimând lungimea arcului unui cerc unitar, stabilește o corespondență între lungimea arcului și măsura gradului său. Acest lucru vă permite să măsurați unghiurile nu numai în grade, ci și utilizând lungimea arcului cercului corespunzător al razei unității. Lungimea arcului se numește măsura radianului unghiului. Unitatea măsurării radianului unghiurilor este radianul. Unghiul unui radian este unghiul pentru care lungimea arcului corespunzător al cercului unității este egală cu una. Măsura gradului unghiului unui radian este

6 Care este lungimea unui cerc? Răspuns. Lungimea unui cerc este numărul la care perimetrele poligoanelor obișnuite înscrise în acest cerc cresc pe măsură ce crește numărul lor.

7 Cum este exprimat perimetrul unui regulat n-gon în funcție de raza cercului circumscris? Răspuns. Perimetrul P n al unui regulat n-gon înscris într-un cerc de rază R este exprimat prin formula
8 Care sunt perimetrele a doi ngoni obișnuiți? Răspuns. Perimetrele n-gonilor obișnuiți sunt considerați ca fiind razele cercurilor circumscrise în jurul lor.
9 Cum se referă la lungimea a două cercuri? Răspuns. Raportul dintre lungimile a două cercuri este egal cu raportul dintre razele lor.
10 Ce înseamnă litera greacă π? Răspuns. Litera greacă π denotă jumătate din lungimea unui cerc de rază a unității.
11 Care este lungimea unui cerc de rază R? Răspuns. Lungimea unui cerc cu raza R este 2πR.
12 Ce inegalități sunt satisfăcute pentru numărul π? Răspuns. Pentru numărul π, inegalitățile
13 Care este valoarea aproximativa a lui π? Răspuns. Valoarea aproximativă a numărului π este considerată a fi 3.14.
14 Care este lungimea arcului cercului la 1 °. Răspuns. Lungimea arcului la 1 o este egală
15 Care este lungimea arcului unui cerc în grade φ? Răspuns. Lungimea l a unui arc cu un cerc de rază R în grade φ va fi exprimată prin formula
16 Care este măsura gradului unghiului unui radian? Răspuns. Măsura gradului unghiului unui radian este
17 Care este lungimea circumferinței circumscrise în jurul unui triunghi echilateral cu latura 1? Soluția. Raza cercului circumscris este egală, astfel încât circumferința este egală cu
18 Cum se va schimba circumferinta daca raza cercului: a) va creste de trei ori; b) reducerea la jumătate? Raspuns: a) va creste de trei ori; b) va scădea la jumătate.
19 Găsiți lungimea cercului descris lângă pătrat cu partea a? răspundă:
20 Găsiți lungimea unui arc dintr-un cerc cu o rază unu, corespunzător unghiului central: a) 30 о; b) 135 °; c) 240 °; d) 315 °. Răspunsul este: a), b); c); g).
21 Care ar trebui să fie raza cercului, în care arcul la 1 o are o lungime de 1 cm? Specificați o valoare aproximativă egală cu un număr întreg de centimetri. Răspuns: cm
22 Răspuns: Cât timp ar trebui să fie o coardă într-un cerc de rază R, astfel încât lungimile arcurilor la care rupe cercul să fie tratate ca 2: 1?
23 Găsiți perimetrul unui regulat n-gon, descris în jurul unui cerc de rază R. Răspuns:
24 După examinarea hexagonilor obișnuiți inscripționați și descriși în jurul circumferinței razei unităților, găsiți limitele inferioare și superioare ale numărului π. Răspuns: 3
25 Într-un cerc de rază R există trei cercuri egale care se ating unii de alții și un anumit cerc. Găsiți raza lor. răspundă:
26 Găsiți măsura radianului unghiurilor în: a) 30 °; b) 45 °; c) 60 o. Răspunsul este: a); b); c).
27 Răspuns: a) 90 o; Găsiți măsura gradului unghiului dacă măsura radianului este: a); b); c); g); d); e). b) 45 °, c) 22 ° 30 '; d) 150 °; e) 70 °, e) 240 °.
28 Găsiți raza globului, pornind de la faptul că 1 m este o valoare de patruzeci de milioane din lungimea ecuatorului. Răspunsul este: m.
Imaginați-vă că globul este acoperit dens cu o frânghie în jurul ecuatorului. Cât durează să crească lungimea frânghiei astfel încât să poată fi ridicată pe toată lungimea pământului cu o distanță de 1 m? Răspuns: La 2 m. M.