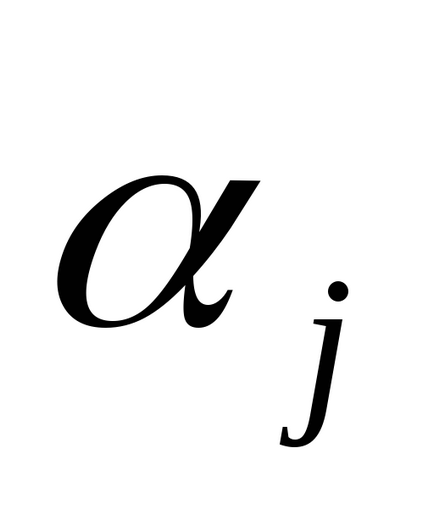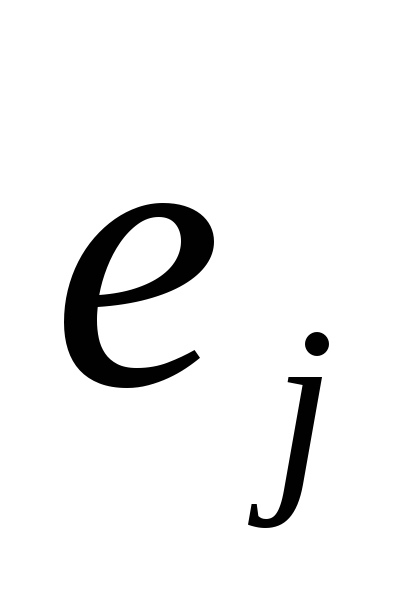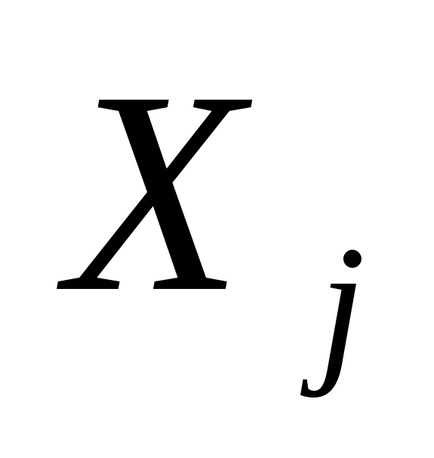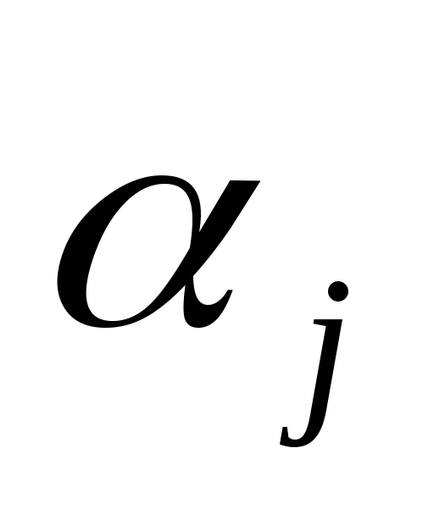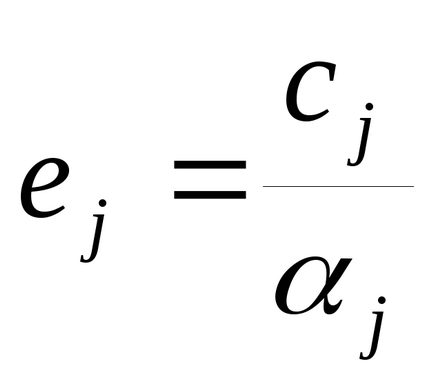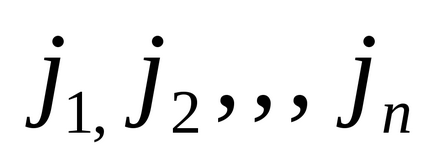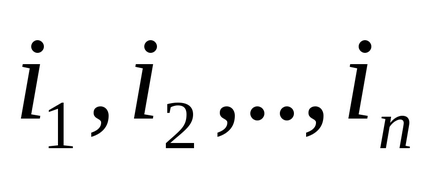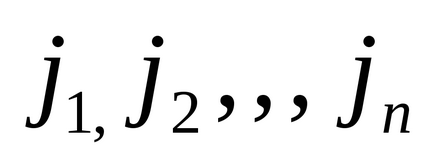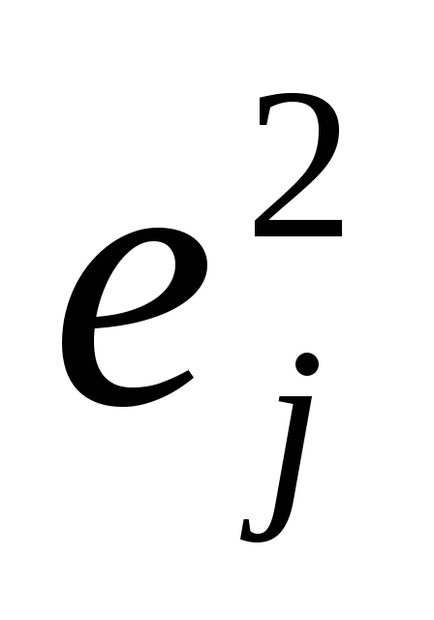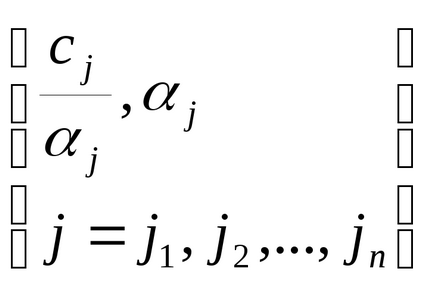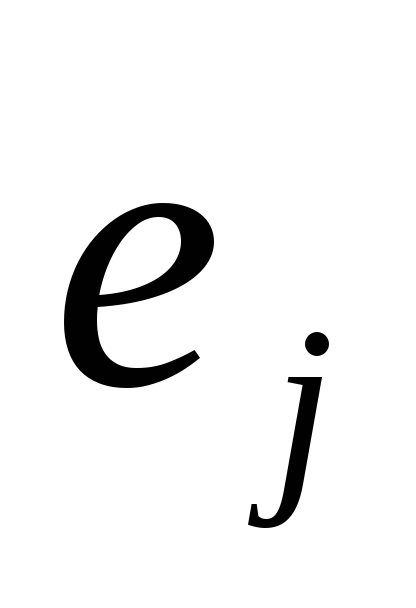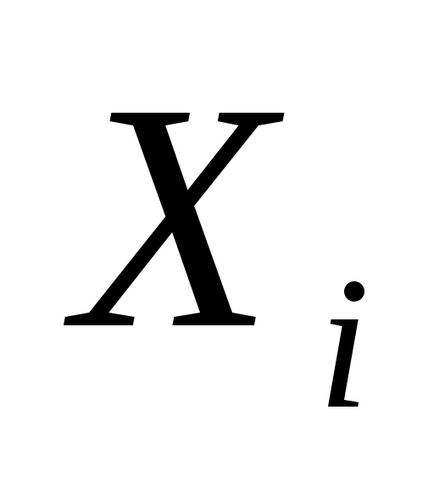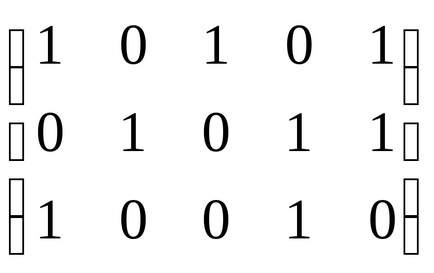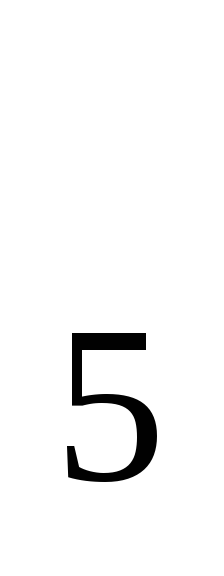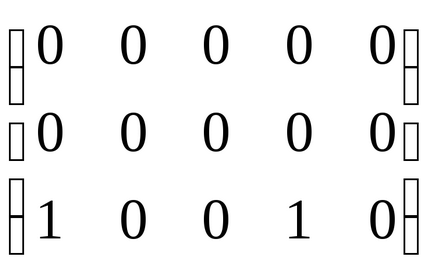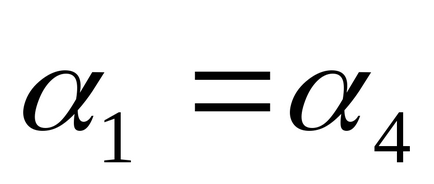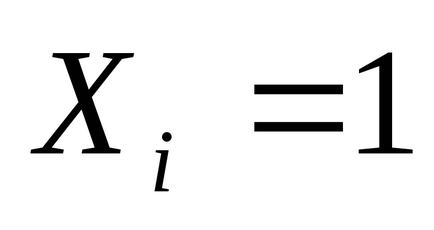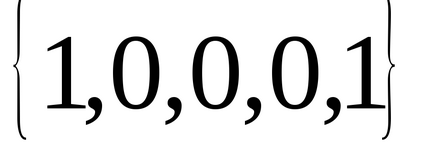lăsa
- numărul de unități din coloana jth,i = 1, m, j = 1, n.
Este necesar să se ia în considerare 2 condiții.
Din moment ce vectorul soluției X este boolean, rezultă din (1): cel mai mic
, cu cât componenta relevantă este mai potrivităpune-l la egal cu 1, j = 1, n.Este de dorit ca variabila pe care o alegem să fie egală cu 1, să intrăm în cât mai multe condiții posibil (2), adică să trecem de la cea mai mare valoare posibilă
,j = 1.n
Luând în considerare acest lucru, introducem relația
,j = 1, n
Pasul 1. Dacă în unele canale de scurgere U1, U2. Unmatricii au numai prima unitate din coloane
, apoi componenta, după cum urmează din (2). Dacă (2) este îndeplinită, atunci sfârșitul. Dacă nu, atunci mergeți la shchag 2.
Pasul 2. În
șterge liniilecoloaneele devin zero. Avem.
=
Notă.
arată că în coloana jnu există un singur vertex, dar corespunde unei componente , cu prețulpoate fi 0 sau 1. Luați în considerare liniile rămase. Înalegeți componenta minimă, permiteți-i să fie, atunci= 1. Dacă mai multe. Le luam pe fiecare pentru o unitate
va arata ca:=
Deoarece min este o componentă, am setat X
= 1
=
Din moment ce C1 cu C4 (
), atunci.
Este ușor de observat că X =
satisface (2.3) și atinge min (1) egal cu 4.
Articole similare