SINTEZA DISPOZITIVELOR DE COMBINARE
Formele canonice de reprezentare a funcțiilor logice.
Sinteza unui dispozitiv logic se descompune în mai multe etape. În prima etapă, aveți nevoie de o funcție definită într-un cuvânt, tabel sau altă formă, reprezentată ca o expresie booleană utilizând o anumită bază. Următorii pași se reduc la obținerea formelor minime de funcții care asigură cel mai mic număr de echipamente electronice în sinteza și construirea rațională a diagramei funcționale a dispozitivului. Pentru reprezentarea inițială a unei funcții, se utilizează de obicei baza AND, OR, OR, indiferent de baza pe care va fi folosită pentru a construi dispozitivul logic.
Următoarele două forme canonice pentru reprezentarea funcțiilor au fost acceptate ca fiind cele inițiale, pentru confortul transformărilor ulterioare: forma normală disjunctivă normală (SDNF) și forma normală conjunctivă normală (SKNF).
^ Forma normală disjunctivă normală (CDNF).
formă normală disjunctivă (DNF) este o formă de reprezentare a unei funcții în care o expresie logică a funcției este construit sub forma unui disjuncție mai multor membri, fiecare dintre acestea fiind o combinație simplă de argumente sau inversiuni lor.
Un exemplu de DNP este expresia
Dăm forma reprezentării funcțiilor care nu sunt DNF. De exemplu, funcția
nu este reprezentată în DNP, deoarece ultimul termen nu este o simplă conjunctură de argumente.
Nici DNP nu este următoarea formă a reprezentării funcției:
Dacă în fiecare termen al DNP sunt reprezentate toate argumentele (sau inversările lor), atunci această formă este denumită formă normală disjunctivă normală (SDNF). Expresia (3.9) nu este un CDNF, deoarece în el doar al treilea termen conține toate argumentele funcției.
Pentru a trece de la DNP la PDNF necesare în fiecare dintre statele membre în care nu toate argumentele, introduceți expresia formei în care xi - absent în argumentul pe termen lung. Deoarece o astfel de operație nu poate schimba valorile unei funcții. Să arătăm trecerea de la DNF la CDNF folosind exemplul expresiei următoare:
Adăugarea unei expresii de formă unui membru va aduce funcția în formular
Pe baza (3.1)
Prin urmare, după reducerea acestor membri:
Forma rezultată este un CDNF. Dacă funcția inițială este dată în formă tabelară, atunci SDNF poate fi obținută direct.
Lăsați o funcție să fie dată sub forma unui tabel. 3.4. Pentru această funcție, SDNF are forma
Așa cum se poate observa din expresia (3.10), în ea fiecare termen corespunde unui anumit set de valori ale argumentelor pentru care funcția
este egal cu 1. Fiecare set de argumente, care se află la 1 (3, 4, 6, 8 seturi de coloane), unitate atrage în termenul corespunzător al expresiei (3.10), în care întreaga funcție este unitatea de Raina.
Este posibilă formularea următoarei reguli pentru înregistrarea SDNF a unei funcții specificate de un tabel de adevăr.
Este necesar să scrieți cât mai mulți membri sub forma conjuncțiilor tuturor argumentelor, câte unități conțin o funcție în tabel. Fiecare conjuncție trebuie să corespundă unui anumit set de valori de argument care ia o funcție la una și dacă valoarea argumentului este zero în acest set, atunci conjuncția argumentului dat este inclusă în conjuncție.
Trebuie remarcat faptul că orice funcție are un SDNF unic.
Forma normală conjunctivă normală (SKNF).
forma normală conjunctivă (CNF) este o formă de reprezentare a unei funcții ca conjuncție cu un număr de membri, fiecare dintre acestea fiind o disjuncție ușor de argumente (sau inversare).
Un exemplu de CNF poate fi următoarea formă a reprezentării funcției:
Dăm forme de reprezentare a funcțiilor care nu sunt CNF:
(aici termenul al treilea nu este o simplă disjuncție a argumentelor sau inversii);
(acest formular nu este, de asemenea, CNF, deoarece în el primul termen nu este conectat la restul operației de conjuncție).
Într-o formă normală conjunctivă perfectă (SKNF), fiecare argument al CNF trebuie prezentat.
Pentru a trece de la CNF la SKNF, trebuie să adăugați membri ai formularului la fiecare membru care nu conține toate argumentele. unde xi este un argument care nu este reprezentat în termen. deoarece
, atunci o astfel de operație nu poate afecta valoarea funcției.
Adăugarea la un membru formează o expresie a formularului. care pot fi reduse la forma
Valabilitatea acestei egalități rezultă din legea distribuției;
De asemenea, se poate afișa prin extinderea parantezelor din partea dreaptă a expresiei:
Luați în considerare trecerea de la CNF la SKIF pe exemplul unei funcții
Să arătăm aplicarea legii distributive pentru realizarea transformărilor utilizate aici peste unul dintre termenii de exprimare
Apoi denotăm prin legea distributivă
Apoi, noi indicăm și aplicăm din nou legea distributivă
Substituind aici valorile z1 și z2, obținem termenii corespunzători expresiei de mai sus pentru tranziția de la CNF la SKNF.
Funcția perfectă CNF este ușor construită din tabelul de adevăr.
Luați în considerare, de exemplu, funcția dată în tabelul. 3.4; SKNF-ul acestei funcții are forma
Expresia conține cât mai mulți membri legați de operatorul de conjuncție, deoarece în tabelul de adevăr există zerouri între valorile funcției f (x1, x2, x3). Astfel, fiecare set de valori de argument pe care funcția este egal cu zero corespunde unui anumit membru CSCN care ia o valoare de zero pe acest set. Deoarece membrii SKNF sunt conectați prin operația de conjuncție, atunci când unul dintre termeni dispare, întreaga funcție este egală cu zero.
Astfel, putem formula următoarea regulă pentru scrierea SKNF a unei funcții specificate de un tabel de adevăr.
Ar trebui să fie scris ca membri conjunctive reprezentând o disjuncție de argumente la cât de multe seturi de valori ale argumentului este egal cu zero, iar în cazul în care valoarea stabilită argumentul este egal cu una, atunci disjungerea intră în inversarea acestui argument. Orice funcție are un singur FCNF.
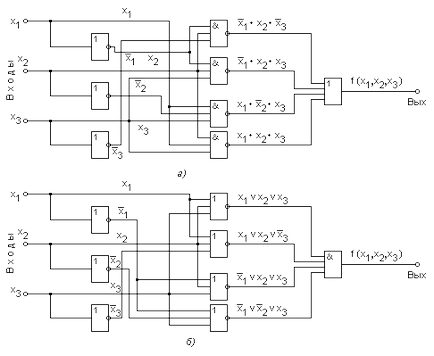
Diagrama bloc a unui dispozitiv logic poate fi construită direct din forma canonică (SDNF sau SKNF) a funcției realizate. Schemele rezultate pentru funcțiile (3.10) și (3.11) sunt prezentate în Fig. 3.26, a și b. Dezavantajul acestei metode de construire a diagramelor bloc, care prevede, în general, funcționarea corectă a dispozitivului este acela că circuitele care rezultă, tind să fie inutil de complexe și necesită un număr mare de elemente logice și, prin urmare, au o eficiență scăzută și fiabilitate.
În multe cazuri, este posibilă simplificarea expresiei logice, astfel încât să nu se încalce funcția, că schema structurală corespunzătoare se dovedește a fi mult mai simplă.
Metodele unei astfel de simplificări a funcțiilor, numite metode de minimizare a funcțiilor, sunt discutate mai jos.
Minimizarea funcțiilor logice prin metoda Quine
Metoda Quine este o astfel de metodă de minimizare funcții booleene care permit reprezintă funcții în DNF sau CNF cu un număr minim de membri și numărul minim de litere în statele. Această metodă cuprinde expresia funcției două faze de conversie: prima tranziție de fază din forma canonică (sau PDNF SKNF) în așa numita formă redusă, doua tranziție de fază a forma redusă a expresiilor logice la forma minimală.
^ Prima etapă (obținerea unui formular redus).
Fie o funcție dată f reprezentată în SDNF.
Trecerea la forma scurtată se bazează pe aplicarea consecventă a două operațiuni: operațiile de lipire și operațiunile de absorbție.
Pentru a efectua operația de lipire, perechile de termeni ai formei și sunt identificate în expresie. diferă doar prin faptul că unul din argumentele din unul dintre termeni este reprezentat fără inversiune, în celălalt cu inversiune. Atunci lipim împreună astfel de perechi de termeni. iar rezultatele lipirii w sunt introduse în expresia funcției ca termeni suplimentari. Apoi se efectuează operația de absorbție. Se bazează pe egalitate
(termenul w absoarbe termenul wz). În realizarea acestei operațiuni, toți membrii absorbiți de membrii care sunt introduși ca rezultat al operației de lipire sunt șterși din expresia logică.
Operațiunile de lipire și absorbție se efectuează secvențial până când execuția lor este posibilă.
Arătăm execuția acestor operațiuni cu privire la funcția prezentată în Tabelul. 3.5.
Notați funcția SDNF
Prin compararea pereche a membrilor (a fiecăruia dintre termeni cu toate cele ulterioare) identificăm perechile de lipire ale termenilor:
primul și al patrulea membru (rezultatul lipirii);
al doilea și al treilea termen (rezultatul lipirii);
al doilea și al patrulea membru (rezultatul lipirii);
al treilea și al cincilea membru (rezultatul lipirii):
al patrulea și al cincilea membru (rezultatul lipirii).
rezultate în exploatare lipirea expresia funcției, introduceți și să efectueze operația de absorbție a membrilor expresiei inițiale: membre absorb acei membri ai expresiei inițiale, care conțin, de exemplu, primul și al patrulea ... Acești membri sunt șterși. Termenul absoarbe a doua și a treia, iar termenul x1 - X3 este al cincilea termen al expresiei originale.
Repetăm operațiunile de lipire și absorbție:
Membru al operațiunii de lipire. Numai doi membri sunt lipiți împreună și. (lipirea împreună a unei perechi de termeni și, conducând la același rezultat), rezultatul lipirii x1. absoarbe al doilea, al treilea, al patrulea și al cincilea termen al expresiei.
Alte operațiuni de lipire și absorbție sunt imposibile, forma scurtă a expresiei pentru o funcție dată (în acest exemplu coincide cu forma minimă)
Membrii formei abreviate (în acest exemplu, acești termeni sunt și x1 sunt numiți implicați simpli ai funcției.
După cum vedem, se obține o expresie mult mai simplă în comparație cu funcția SDNF.
În Fig. 3.27 este o diagramă bloc a unui dispozitiv logic în baza AND, OR, HE, construită folosind expresia (3.13).
^ A doua etapă (obținerea formei minime).
Forma abreviată poate conține termeni suplimentari, excepția căruia din expresia funcției nu va afecta valoarea funcției.