Funcțiile inversoare trigonometrice (arcsina, arcul cosinus, arctangent și arccotangent) sunt funcțiile elementare de bază. Adesea, datorită prefixului "arc", funcțiile trigonometrice inverse sunt numite funcții arc. Acum ne vom uita la graficele lor și vom lista proprietățile.
Funcția sinusoidală arc este y = arcsin (x).
Reprezentăm graficul funcției sinusoidale:
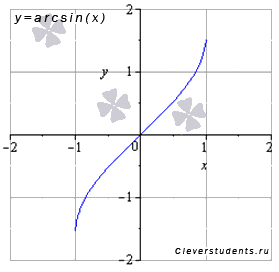
Proprietățile funcției sinusoidale arc y = arcsin (x).
· Domeniul de definire a funcției sinusoidale arc este intervalul de la o unitate la alta, inclusiv :.
· Intervalul funcției y = arcsin (x). .
· Funcția arcsine este ciudată, deoarece.
· Funcția y = arcsin (x) crește pe întregul domeniu, adică la.
· Funcția este concavă când. convex la.
· Punct de inflexiune (0; 0). este o funcție zero.
Înapoi la început
Funcția cosinus arc y = arccos (x).
Graficul grafic al funcției cosinus arc arata astfel:
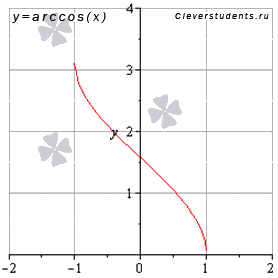
Proprietățile funcției cosinusului arc y = arccos (x).
· Zona de definire a funcției cosinusului arc :.
· Intervalul funcției y = arccos (x). .
· Funcția nu este ciudată sau ciudată, adică este de un gen general.
· Funcția cosinus arc scade în întregul domeniu de definiție, adică când.
· Funcția este concavă când. convex la.
Înapoi la început
Funcția tangentă arc y = arctg (x).
Graficul grafic al funcției arctangent are forma:
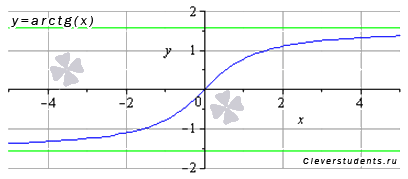
Proprietățile funcției tangente arc y = arctg (x).
· Domeniul funcției y = arctg (x). .
Intervalul funcției arctangent :.
· Funcția tangentă arc este ciudată, deoarece.
· Funcția crește pe întregul domeniu al definiției, adică când.
· Funcția concavă arctangentă. convex la.
· Punct de inflexiune (0; 0). este o funcție zero.
· Asimptotele orizontale sunt linii drepte pentru și pentru. În desen sunt afișate în verde.
Înapoi la început
Funcția arccotangentă y = arcctg (x).
Reprezentăm graficul funcției arccotangent:
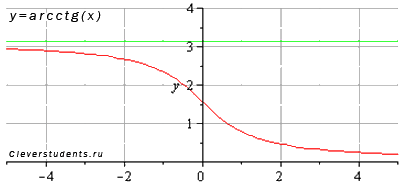
Proprietățile funcției arccotangente y = arcctg (x).
· Gama funcției arccotangent este întregul set de numere reale :.
· Intervalul funcției y = arcctg (x). .
· Funcția arccotangentă nu este ciudată sau ciudată, adică are un caracter general.
· Funcția scade pe întregul domeniu, adică când.
· Funcția este concavă când. convex la.
· Asimptotele orizontale sunt linii drepte atunci când (în figură este afișată în verde) și y = 0 pentru.