Metoda Metropolis a fost prezentată ca un proces Markov în care o plimbare aleatorie a fost construită astfel încât probabilitatea de a găsi un anumit punct este proporțională cu factorul Boltzmann. Există multe modalități de a construi o astfel de plimbare aleatoare. În conformitate cu schema Metropolis, acest sistem este următorul:
Particula este aleasă aleatoriu și se calculează energia ei U ().
Particula se deplasează pe o distanță scurtă în direcția aleatorie r '= r + Δ. Aceasta duce la o schimbare a potențialului de energie al sistemului cu o anumită valoare a ΔU. Energia particulelor este acum U ().
Mutarea de la este acceptată cu probabilitate
. ()
Există mai multe tipuri de deplasări în metoda MC [9]:
Rotația moleculei în jurul unei axe alese aleatoriu;
Schimbarea volumului (ansamblul Gibbs și NPT);
Mutarea unei molecule de la o celulă la alta (ansamblul Gibbs);
Distrugerea unei molecule existente sau introducerea unei noi molecule (Grand Canal Ensemble);
Creșterea oricărei părți a moleculei (pentru moleculele flexibile);
Flip, adică rotația unui atom în jurul axei formate de vecinii săi imediate (pentru molecule flexibile);
Refacerea, adică îndepărtarea unui capăt al moleculei și creșterea celuilalt capăt (pentru moleculele flexibile);
Permutarea, adică îndepărtarea unei molecule și plasarea unei alte molecule în locul ei;
Rotația unei părți a unei molecule în jurul unui atom (pentru molecule flexibile);
Toate aceste mișcări sunt necesare pentru a ține cont de toate configurațiile posibile dintr-un ansamblu dat, precum și de toate orientările posibile, pozițiile și conformitățile interne. Figura 2 prezintă toate mișcările posibile din ansamblul Gibbs.
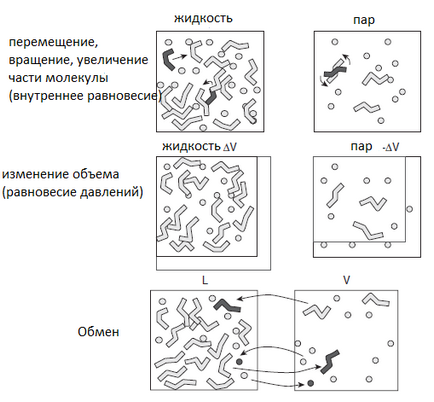
Figura 2. Principiile ansamblului Gibbs. Două celule simulate sunt utilizate pentru a reprezenta fazele în echilibru. Mișcările interne (mișcări, rotații și măriri) sunt folosite pentru menținerea echilibrului termic la o temperatură constantă. Schimbarea volumului este folosită pentru a obține un echilibru al presiunilor, iar schimbul de molecule este folosit pentru a menține un echilibru chimic între cele două faze [9].
Ansamblul statistic
Un ansamblu statistic al unui sistem fizic este un set al tuturor stărilor posibile ale unui sistem dat care îndeplinesc anumite criterii. Alegerea unui ansamblu statistic pentru modelarea moleculară este un punct cheie și primordial. Pur și simplu, ansamblul statistic selectat ia în considerare posibilele stări ale sistemului în combinație cu anumite constrângeri (temperatura constantă, numărul particulelor, presiunea etc.) [19]. Și parametrii care nu au fost stabiliți, au fluctuații. Ansamblurile statistice utilizate în modelarea moleculară sunt prezentate în tabelul 1. După cum se poate observa din acest tabel, pe baza obiectivelor, se alege un ansamblu statistic. Fiecare ansamblu statistic este caracterizat de densitatea de probabilitate, adică de probabilitatea apariției fiecărei stări a sistemului în agregat.
Tabelul 1. Ansamblurile statistice utilizate în modelarea moleculară [9].
Considerăm ansamblul canonic. Aceasta corespunde unui sistem fizic care schimbă energia cu mediul, fiind în echilibru termic cu el. În acest caz, parametrii constanți sunt volumul, numărul de particule și temperatura. Funcția de partiție
unde este lungimea de undă termică de Broglie. Din suma statistică rezultă că probabilitatea de a găsi o configurație este supusă distribuției:
Aceste două ecuații sunt de bază atunci când se modelează folosind ansamblul canonic.
Simularea folosind ansamblul canonic are loc în conformitate cu următoarea schemă:
O particulă este aleasă aleatoriu și se calculează energia acestei configurații U (0).
Particula se deplasează la o distanță aleatorie,
,
unde este deplasarea maximă. Noua configurație este notată cu energia ei U (n).
Mutarea este acceptată cu probabilitate:
.
Energia suferă fluctuații, adică setul conține stările sistemului la diferite energii. Cu toate acestea, putem calcula energia medie (unde m este numărul de stări ale sistemului din ansamblu), care pot fi comparate cu datele experimentale, de exemplu, utilizând energia molară:
unde este numărul Avogadro și N este numărul total de particule din sistem.
Isotherm - ansamblul isobaric al NTP. în care, în loc de un volum, presiunea este menținută constantă. Acest ansamblu este foarte des folosit, deoarece cele mai multe experimente sunt efectuate la presiune și temperatură controlată. Să presupunem că sunt considerați N atomi identici. Suma statistică are forma:
Selectarea se poate face conform regulii:
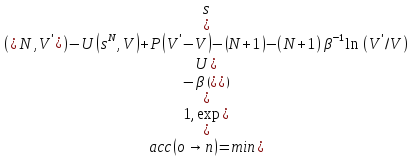
O descriere mai detaliată poate fi găsită în [17].
Ansamblurile discutate mai sus au avut un număr constant de particule, dar uneori este necesar să se obțină informații despre numărul mediu de particule în funcție de condițiile externe, de exemplu în studiile de adsorbție în solide poroase. În acest scop, este recomandabil să se folosească Marele Ansamblu Canonical (BKA). în care parametrii constanți sunt temperatura, volumul și potențialul chimic al tipului de molecule μjj. Pentru acest ansamblu, suma statistică are forma:
Iar densitatea de probabilitate corespunzătoare:
.
Probabilitatea de a face o mutare:
.
În acest caz, particula este plasată într-o poziție aleatorie sau este îndepărtată o particulă selectată aleator. Formarea particulelor se presupune cu probabilitate:
,
iar îndepărtarea particulei este luată cu probabilitate
.
Deci, fiecare microstat este o celulă simulată care conține materialul poros investigat și configurația moleculelor adsorbite, determinată de T și μ. În aceste condiții, BCA permite densitatea și energia fluctuantă, cu o selecție de micro-stații, și se calculează valorile medii ale parametrilor fluctuanți. Ca rezultat, izoterma adsorbției este densitatea (sau numărul mediu de molecule adsorbite) a potențialului chimic la o temperatură constantă. Generarea microstațiilor se bazează pe procesul Markov, adică pentru orice configurație moleculară dată, se generează următoarele prin comutarea aleatorie, îndepărtarea sau mutarea moleculei adsorbite. În cazul în care moleculele nu sunt sferice, atunci toate mișcările sunt însoțite de o rotație aleatorie [20]. Ansamblul cel mai adesea folosit pentru calcularea parametrilor de echilibru al fazei este ansamblul Gibbs [21]. Două faze sunt reprezentate în două celule simulate separate. Există două modalități de modelare: cu un volum constant constant de două faze sau cu o presiune constantă. În același timp, temperatura și numărul de particule sunt considerate a fi constante. Când se ia în considerare sistemele pure, ansamblul este utilizat la un volum constant, în timp ce datele de ieșire pot fi presiunea saturată a vaporilor, entalpia evaporării sau densitatea lichidului și a vaporilor. În cazul amestecurilor, ansamblul Gibbs poate fi utilizat fie la presiune constantă, fie la un volum constant. În ambele cazuri, se mențin compozițiile de echilibru și densitățile fazelor coexistente. Energia sistemului molecular
Se știe că energia unui sistem molecular constă în energia cinetică K și potențială U. În dinamica moleculară, soluția ecuațiilor de mișcare în fiecare moment al timpului face posibilă calcularea energiei cinetice în fiecare moment al timpului și medierea energiei cinetice ne va permite să determinăm temperatura sistemului. Prin simularea Monte Carlo, temperatura este constantă și relația sa cu energia cinetică este utilizată pentru a calcula contribuția energiei cinetice la ansamblu. În ambele cazuri, este important să se calculeze energia potențială din coordonatele moleculelor. Energia potențială constă din două componente: intramoleculare și intermoleculare. Energia potentialului intermolecular, la rândul său, constă în energia Lennard-Jones, energia electrostatică și energia de polarizare. Energia Lennard-Jones, care predomină în sistemele cu un polar scăzut, cum ar fi alcani (cu formula generală CnH2n + 2), are forma:
unde este distanța dintre centrele de putere. Parametrii energiei potențiale Lennard-Jones sunt descriși în tabelul 2.
Un model de potențială energie care tratează atomii individuali ca centre de putere Lennard-Jones este numit "AllAtoms" sau "all atoms" [22. 23 24]. Dacă centrul de forță se află într-un atom dintr-un grup de atomi, atunci un astfel de model este numit "UnitedAtoms" sau "atoms combined" [25. 26. 27]. Cel de-al treilea model este "atomi uni anizotropi" sau "atomi uniti anizotropici", în care centrul forței poate fi în spațiul dintre un anumit grup de atomi (Figura 3) [28 29] Energia electrostatică este definită de expresia:
, unde sumarea este peste toate perechi posibile de molecule cu sarcini q și separate de o distanță, - constantă electrostatică.
Energia de polarizare se formează datorită deformării noriilor electronice ale moleculelor sub acțiunea moleculelor polare sau solide din jur. De obicei, în calcule se înțelege că această energie este luată în considerare indirect în energia Lennard-Jones sau în energia electrostatică.
Energia interacțiunii intramoleculare constă în energiile de tensiune, îndoire și torsiune. Întinderea este asociată cu o modificare a lungimii legăturii l. pliate cu o schimbare a unghiului dintre două legături, și torsiune cu o schimbare a unghiului diedural φ (Figura 4).
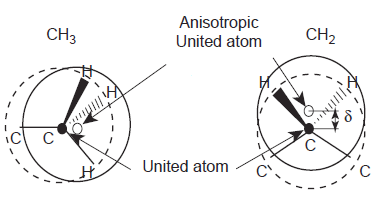
Figura 3. Principiul potențialului intramolecular al atomilor uniți anizotropici (AUA) și potențialul atomilor uniți (UA). În primul caz, centrul de putere AUA este situat în apropierea centrului geometric al sistemului, în al doilea caz centrul de putere al UA se află în nucleul atomului de carbon [9].
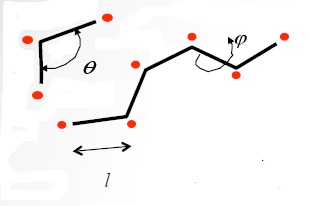
Figura 4. Parametrii unei molecule flexibile
Aceste energii potențiale sunt calculate conform următoarelor formule:
energia de îndoire, (32)
torsiune, (33)
și energia de întindere se calculează utilizând potențialul Lennard-Jones (formula 44)
Dacă molecula este flexibilă, atunci însumarea are loc la toate unghiurile și perechi de centre de forță separate de mai mult de trei legături. Dacă molecula este considerată rigidă, atunci aceste contribuții nu sunt luate în considerare în procesul de calcul. Trebuie de asemenea remarcat faptul că alte expresii pot fi folosite în locul expresiilor (45) și (46), iar motivul principal al preferințelor (45) și (46) este acela că mai puțin timp de calcul este cheltuit în calculul acestora [30].
/