Punctele corpului care se rotesc în jurul axei se deplasează de-a lungul cercurilor (Figura 30, a), ale căror raze sunt egale cu distanțele punctelor de la axa de rotație.
Viteza liniară V a punctului A și viteza unghiulară # 969; organismele sunt conectate unul cu celălalt în mod liniar
Înlocuind în formula pentru viteza liniară a punctelor corpului care se rotesc în jurul axei fixe, valoarea n a vitezei unghiulare în rotații pe minut, obținem
Direcționat perpendicular pe raza r în lateral # 969; (Figura 30, a).
În general, vectorul de viteză al punctului A. care se rotește în jurul punctului O variază în funcție de magnitudine și direcție. Prin urmare, acest punct va avea o accelerație normală (caracterizează schimbarea direcției) și accelerația tangențială (caracterizează schimbarea în magnitudine). Valoarea accelerației normale a punctului A este definită ca
Substituind în această expresie valoarea vitezei vA = # 969; r. avem
Acesta este îndreptat de-a lungul razei r spre centrul O de rotație.
Accelerarea tangențială a unui punct este determinată de exprimare
unde # 949; Anglare accelerată a unui corp rotativ.
Trimise perpendicular r în lateral # 949;.
Accelerarea completă a punctului cu rotație neuniformă în jurul axei (Figura 30, b) este compusă geometric din accelerațiile tangențiale și normale
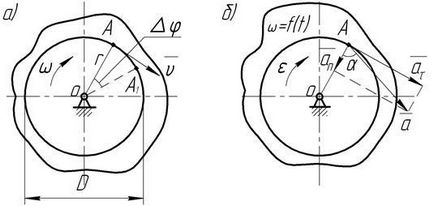
Fig. 30. Velocitățile și accelerațiile punctului unui corp rotativ.