Orice date pot fi atribuite uneia din cele două tipuri: bază (simplă), a cărei formă de reprezentare este determinată de arhitectura calculatorului sau complexă, proiectată de utilizator pentru a rezolva anumite probleme.
Datele unui tip simplu sunt simboluri, numere și așa mai departe. elemente, a căror fragmentare ulterioară nu are sens. Din datele elementare se formează structuri (tipuri complexe) de date.
· Array (funcție cu domeniul de aplicare finit) - o colecție simplă de elemente de date de același tip, un mijloc de operare a unui grup de date de același tip. Un singur element al matricei este specificat de un index. O matrice poate fi una-dimensională, bidimensională și așa mai departe. Soiurile de rețele unidimensionale cu lungime variabilă sunt structuri precum inel, coș, coadă și coadă în două direcții.
· Record (produs cartezian) - o colecție de elemente de date de diferite tipuri. În cel mai simplu caz, înregistrarea conține un număr constant de elemente, numite câmpuri. O colecție de înregistrări cu aceeași structură se numește fișier. (Un fișier este, de asemenea, numit un set de date în memoria externă, de exemplu, pe un disc magnetic). Pentru asta. Pentru a putea extrage înregistrări individuale dintr-un fișier, fiecărei intrări li se atribuie un nume sau un număr unic care servește ca identificator și se află într-un câmp separat. Acest identificator este numit o cheie.
Astfel de structuri de date cum ar fi o matrice sau o înregistrare ocupă un volum constant în memoria calculatorului, prin urmare ele sunt numite structuri statice. Structurile statice sunt de asemenea multe.
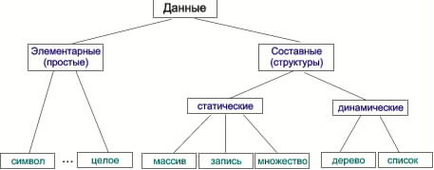
Fig. 1.1. Clasificarea tipurilor de date
Deasupra am considerat mai multe tipuri de structuri care sunt colecții de elemente de date: o matrice, un arbore, un record. Un tip de date mai complex poate include aceste structuri ca elemente. De exemplu, elementele unei înregistrări pot fi o matrice, un teanc, un copac etc.
Există o mare varietate de tipuri complexe de date, însă studiile efectuate pe un material practic mare au arătat că printre acestea există mai multe dintre cele mai comune. Structurile generalizate sunt, de asemenea, numite modele de date. deoarece ele reflectă viziunea utilizatorului asupra datelor din lumea reală.
Orice model de date trebuie să conțină trei componente:
1. Structura datelor - descrie punctul de vedere al utilizatorului asupra reprezentării datelor.
2. Un set de operațiuni admise. executate pe structura de date. Modelul de date presupune, cel puțin, prezența unei limbi de definiție a datelor (JOD) care descrie structura stocării acestora și un limbaj de manipulare a datelor (NAM), inclusiv operațiile de extragere și modificare a datelor.
3. constrângeri de integritate - mecanismul de menținere a corespondenței datelor în domeniu pe baza regulilor descrise în mod formal.
În procesul de dezvoltare istorică, în SGBD s-au utilizat următoarele modele de date:
Recent, o abordare tot mai orientată spre obiect a reprezentării datelor a devenit din ce în ce mai importantă.
Problemele reprezentării datelor sunt strâns legate de operațiunile prin care aceste date sunt procesate. Astfel de operațiuni includ: prelevarea de probe, schimbarea, includerea și excluderea datelor. În centrul tuturor acestor operațiuni este o operație de acces. care nu pot fi luate în considerare indiferent de modul de prezentare.
În sarcinile de căutare, se presupune că toate datele sunt stocate în memorie cu o anumită identificare și, în ceea ce privește accesul, înseamnă mai întâi accesul la date (numite chei) care identifică în mod unic seturile de date asociate.
Să presupunem că trebuie să organizăm accesul la un fișier care conține un set de înregistrări identice, fiecare având o valoare unică pentru câmpul cheie. Cea mai ușoară modalitate de căutare este de a scana secvențial fiecare intrare din fișier până când găsiți cheia a cărei valoare corespunde criteriilor de căutare. Evident, această metodă este foarte ineficientă, deoarece intrările din fișier nu sunt ordonate de valoarea câmpului cheie. De asemenea, sortarea înregistrărilor din fișier nu este aplicabilă, deoarece este nevoie de mai mult timp și ar trebui făcută după fiecare adăugare a înregistrării. Prin urmare, procedați după cum urmează: cheile împreună cu indicii către intrările corespunzătoare din fișier sunt copiate într-o altă structură, ceea ce vă permite să efectuați rapid operații de sortare și căutare. La accesarea datelor, valoarea principală corespunzătoare se găsește mai întâi în această structură, iar apoi se obține o înregistrare a indicelui din fișier folosind indicatorul stocat cu acesta.
Există două clase de metode care implementează accesul la date prin cheie:
· Metode de căutare a copacului,
Metode de căutare pentru un arbore
Definiție: Un arbore este un set finit format din unul sau mai multe elemente numite noduri, astfel încât:
1. Între noduri există o relație de tip "generat inițial";
2. există un singur nod care nu are nodul sursă. Se numește rădăcină;
3. Toate nodurile, cu excepția rădăcină, au o singură sursă; fiecare nod poate avea mai multe noduri copil;
4. relația "generată inițial" acționează numai într-o direcție, adică nici un descendent al unui anumit nod nu poate deveni un strămoș pentru el.
Numărul de noduri individuale generate (numărul de subtreri dintr-o rădăcină dată) se numește gradul său. Un nod cu un grad zero este numit o frunză sau un nod terminal. Valoarea maximă a gradului tuturor nodurilor unui copac dat se numește gradul copacului.
Dacă în arborele dintre nodurile generate care au o sursă comună, ordinea lor este considerată esențială, atunci arborele se numește ordonat. Sarcinile de căutare aproape întotdeauna iau în considerare copaci ordonați.
Un copac ordonat al cărui grad este cel mult 2 se numește arbore binar. Un arbore binar este folosit în mod special pentru căutarea în memorie. Algoritmul de căutare: în primul rând, argumentul de căutare este comparat cu cheia de la rădăcină. Dacă argumentul este același ca și cheia, căutarea este terminată, în cazul în care nu același lucru, în cazul în care argumentul este mai mică decât cheia, căutarea continuă în subarborele stâng, iar în cazul în care mai cheie - în subarborelui drept. Creșterea nivelului cu 1, repetați comparația, presupunând că nodul curent este rădăcina.
Exemplu: Să se prezinte lista studenților care conțin numele lor de familie și scorul mediu de performanță (vezi Tabelul 1.1). Numele de familie al elevului este folosit ca o cheie. Să presupunem că toate înregistrările au o lungime fixă, apoi poți folosi numărul de înregistrare ca un pointer. Deplasarea înregistrării din fișier în acest caz va fi calculată ca ([record number] -1) * [length of record]. Lăsați argumentul de căutare "Petrov". Figura 1.2 prezintă unul din arborele de căutare binar posibil și calea de căutare pentru acest set de date.
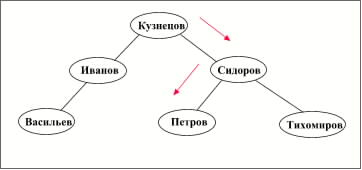
Fig. 1.2. Căutați după copac binar
Rețineți că aici este utilizată următoarea regulă pentru compararea variabilelor de șir: se presupune că valoarea unui simbol corespunde numărului său ordinal în alfabet. Prin urmare, "I" este mai mic decât "K", iar "K" este mai mic decât "C". Dacă se potrivesc caracterele curente din liniile comparate, atunci simbolurile din următoarele poziții sunt comparate.
Binocerii binari sunt deosebit de eficienți atunci când o mulțime de chei sunt necunoscute în prealabil sau când acest set se schimbă intens. Este evident că, cu un set variabil de chei, este mai bine să ai un copac echilibrat.
Definiție: Un copac binar este considerat a fi echilibrat dacă înălțimea substratului stâng al fiecărui nod diferă de înălțimea subtreei drepte cu nu mai mult de 1.
Când căutați date în memoria externă, este foarte important să reduceți numărul de transferuri de date de la memoria RAM la memoria RAM. Prin urmare, în acest caz, în comparație cu arborii binari, arborii cu ramificație foarte mare se vor dovedi a fi mai profitabili. înălțimea lor este mai mică, atunci căutarea va necesita mai puțin acces la memoria externă. Cea mai mare aplicație în acest caz a fost B-arborii (B-echilibrat)
Definiție: Un arbore B de ordinul n este un arbore puternic de ramificație de grad 2n + 1 cu următoarele proprietăți:
- Fiecare nod, cu excepția rădăcină, conține cel puțin n și nu mai mult de 2n chei.
- Rădăcina conține cel puțin una și nu mai mult de 2n chei.
- Toate frunzele sunt la același nivel.
- Fiecare nod intermediar conține două liste: o listă de chei ordonate în ordine crescătoare și o listă corespunzătoare de indicatori (nu există o listă de indicatori pentru nodurile frunzelor).
Pentru un astfel de copac:
• Accesul secvențial poate fi organizat comparativ ușor, deoarece toate frunzele sunt la același nivel;
· La adăugarea și modificarea cheilor, toate modificările sunt, de regulă, limitate la un singur nod.
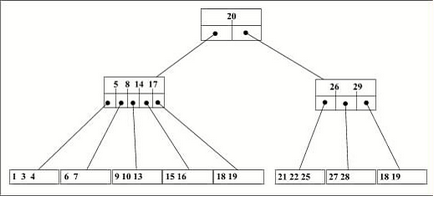
Fig. Copacul echilibrat
Într-un arbore în care adevăratele valori sunt cuprinse numai în frunze (nodurile finale), se numește arborele B +. Nodurile interne ale unui astfel de arbore conțin delimitatorii care specifică intervalul modificărilor cheie pentru subtreturi.
Arborele R (R-Tree) este structura indexului pentru accesarea datelor spațiale, propusă de A. Guttman (Universitatea din California, Berkeley). R-tree-ul permite executarea arbitrară a operațiilor de adăugare, ștergere și recuperare a datelor fără reindexare periodică.
Pentru a reprezenta datele, se utilizează înregistrări, fiecare având un identificator unic (identificator-tuplu). Fiecare nod de sfârșit (arbore) al arborelui conține o înregistrare a formularului (I, tuple-identifier). unde I - (. De asemenea, numit minimal dreptunghi de delimitare MBR) n paralelipiped -dimensional conținând indicii pentru date spațiale, și fiecare element din tuple-identificator cuprinde un superior și inferior legat de dimensiunea corespunzătoare a paralelipipedului.
Nodurile non-terminale conțin înregistrări ale formularului (I, indicator de copil-indicator). unde I este caseta de margine minimă pentru MBR a tuturor nodurilor derivate în legătură cu aceasta. Indicatorul pentru copii de nod este un indicator pentru nodurile derivate.
Lăsați M și m<= M/2 соответственно максимальное и мимимальное количество элементов, которое может быть размещено в узле. Тогда свойства R-дерева можно описать следующим образом:
· R-Tree este un copac foarte echilibrat, adică toate frunzele sunt la același nivel.
· Nodul rădăcină are cel puțin doi copii.
Pentru fiecare element (I, indicator de copil-nod) într-un nod neterminal, I este cea mai mică cutie posibilă, adică conține toate paralelipipedele nodurilor derivate.
· Fiecare nod final (foaie) conține de la m la M înregistrări index.
· Pentru fiecare înregistrare de index (I, tuple-identifier) în nodul final I este un paralelipiped care conține obiectul de date n-dimensional indicat de identificatorul tuple.
1.2.2 Hashing
Baze de date Dump Database