Să facem experimentele. La fascicul de solzi atarna doua bile identice. Greutatea lor este aceeași, astfel încât fasciculul este în echilibru (figura "A"). Înlocuim un pahar gol sub sfera dreaptă. Din aceasta, greutatea bilelor nu se va schimba, astfel încât echilibrul va rămâne (figura B).
Umpleți sticla cu dioxid de carbon, a cărui densitate este mai mare decât densitatea aerului (fig. "C"). Echilibrul va fi rupt, arătând că greutatea mingii din dreapta a devenit mai mică. Acest lucru sa întâmplat deoarece o mare forță arhimedeză acționează asupra sferei în gaze cu dioxid de carbon decât în aer.
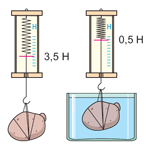
A doua experiență. Vom atașa un cartof mare la dinamometru. Veți vedea că greutatea sa este de 3,5 N. Vom încărca cartofii în apă. Se constată că greutatea sa a scăzut și a ajuns la 0,5 N.
Să calculăm schimbarea în greutatea cartofului:
De ce a scăzut greutatea cartofilor cu exact 3 N? Se pare că, în apă, potența a fost afectată de forța de împingere de aceeași mărime. Cu alte cuvinte, puterea lui Archimedes este egală cu modificarea greutății corporale:
Această formulă exprimă modul de măsurare a forței Archimedean: trebuie să măsurați greutatea corpului de două ori și să calculați schimbarea. Valoarea obținută este egală cu puterea lui Archimedes.
Pentru a deduce următoarea formulă, să facem experimentul cu dispozitivul "Archimedes bucket". Piesele sale principale sunt următoarele: un arc cu o săgeată 1, o găleată 2, un corp 3, un vas de turnare 4, o ceașcă 5.
În primul rând găleată și corpul de primăvară suspendat de un trepied (fig. „A“) și marchează poziția mărcii săgeți de culoare galbenă. Apoi, corpul este plasat într-un vas de reflux. Pe măsură ce vă scufundați, corpul deplasează un anumit volum de apă. care se îmbină într-un pahar (figura b). Greutatea corporală devine mai mică, astfel încât primăvara se contractă, iar săgeata se ridică deasupra semnei galbene.
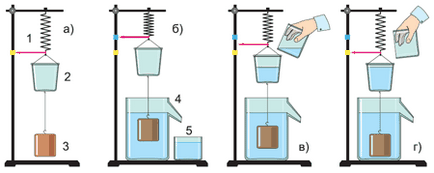
Vom turna apa deplasată de corp în cuvă (fig. "C"). Cel mai uimitor lucru este că, atunci când apa este transfuzat (Figura „d“), săgeata nu se încadrează doar în jos, și indică exact pe etichetă galbenă! Prin urmare, greutatea turnată în galeata echilibrată a apei Archimedean.
Sub forma unei formuli, această concluzie este scrisă după cum urmează:
Rezumând rezultatele experimentului, obținem Arhimede: forța dinamică care acționează asupra corpului în lichid (sau gaz) este egală cu greutatea lichidului (gaz) luate într-un volum al corpului și direcționat opus vectorului greutății sale.
Arhimede forța de calcul
În paragraful anterior, am numit două formule prin care puterea lui Archimedes poate fi măsurată. Acum derivăm o formulă prin care se poate calcula forța lui Arhimede.
Legea lui Archimedes este exprimată prin formula (vezi §3-e):
Să presupunem că greutatea lichidului deplasat este egală cu forța gravitațională care acționează asupra lui:
Masa lichidului deplasat poate fi găsită din formula pentru calculul densității:
Înlocuindu-ne formulele în ele, obținem egalitatea:
Să scriem începutul și sfârșitul acestei egalități:
Reamintim că legea lui Archimedes este valabilă pentru lichide și gaze. Deci, în loc să se refere la „# 114; g "este mai corect de a utiliza denumirea" # 114; g # 47; d“. De asemenea, rețineți că volumul de lichid deplasat de corp este exact egal cu volumul părții corpului scufundat # 58; - # 86; x - # 61; Luând în considerare aceste îmbunătățiri, obținem:
au dedus un caz special al legii lui Archimedes - o formulă care exprimă o modalitate de calcul al puterii lui Archimedes. Vă întrebați: de ce este această formulă un "caz special", adică mai puțin general?
Să explicăm un exemplu. Imaginați-vă că efectuăm experimente într-o navă spațială. Conform formulei # 70; arkh - # 87; g. forța arhimediană este zero (deoarece greutatea lichidului este zero), conform aceleiași formule Fapx = # 114; ж / гgVпч Forța arhimedei nu este egală cu zero, deoarece nici una dintre cantități # 44; # 44; - # 103; # 44; - # 86; ) în greutate zero la zero nu se aplică. Trecând de la experimentele imaginare până în prezent, vom vedea că formula generală este justificată. # 70; arc - # 70; - # 70; grele
Împărțiți partea stângă și cea dreaptă a ecuației cu coeficientul "g":
Reamintind asta # 109; - # 114; - # 114; # 86 ;. obținem egalitatea:
Transformăm această ecuație într-o proporție:
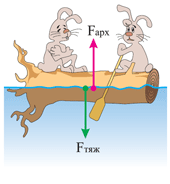
În partea stângă a raportului există o fracțiune care arată fracțiunea care este volumul părții scufundate a corpului din volumul întregului corp. Prin urmare, întreaga fracțiune se numește fracțiunea ponderată a corpului:
Folosind această formulă, vom anticipa ce ar trebui să fie egal cu cota jurnalului scufundat când înotați în apă:
PDT (bușteni) "- 500 kg / m3 3. 1000 kg / m3 = 0,5
Numărul 0.5 înseamnă că jurnalul plutitor este scufundat în jumătate. Acest lucru este prezis de teorie, iar acest lucru coincide cu practica. Deci, ambele formule din cadrul sunt mai puțin generale decât cele originale, adică au limite mai restrânse de aplicabilitate. De ce sa întâmplat asta? Motivul este că folosim formula W = Fraction. Amintiți-vă că nu este adevărat dacă corpul și sprijinul său se deplasează indirect (a se vedea §3-d). Nava spatiala se misca in acelasi mod - intr-o orbita circulara in jurul Pamantului.