Într-adevăr, balamaua "nu va permite" corpului să se deplaseze în ansamblu în orice direcție, astfel încât forța reacției articulației este direcționată astfel încât să compenseze forțele rămase care acționează asupra corpului. Această condiție ne permite să găsim forța de reacție a balamalei.
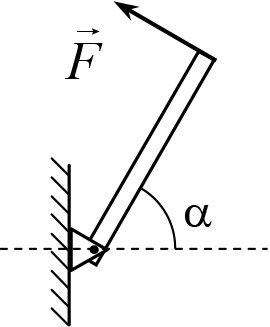
Exemplul 16.4. Un capăt al tijei având masa m. este atașat la peretele vertical printr-o balama. La cel de-al doilea capăt al tijei este aplicată o forță F direcționată perpendicular pe tija. În echilibru, unghiul dintre tijă și orizont este egal (figura 16.7). Găsiți forța reacției balamalei.
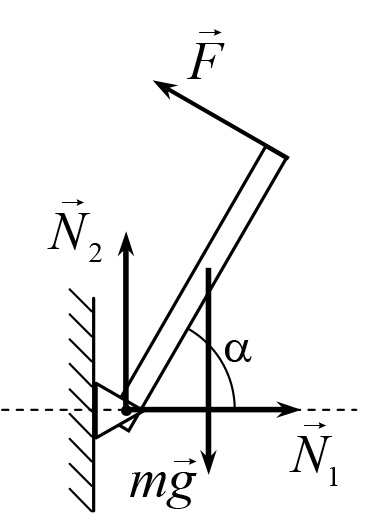
Soluția. Tija este acționată prin: gravitatea m (aplicată în centrul tijei), forța exterioară și forța din partea balamalei. Deoarece direcția forței de reacție nu ne este cunoscută, este convenabil să descompunem această forță în două componente reciproc perpendiculare (orizontală și verticală, Figura 16.8) și să le căutăm separat unele de altele. Se dă condiția pentru egalitatea sumelor momentelor legate de balamale
(în mod evident, momentele ambelor componente ale forței de reacție față de balama sunt zero). Din ecuația (16.6) găsim forța F. asigurând echilibrul tijei
Acum, din condiția ca suma forțelor care acționează asupra tijei (pentru proiecții orizontale și verticale) să fie zero, găsim componentele forței cu care balama acționează asupra tijei
Forța totală a reacției articulației poate fi găsită de teorema lui Pitagora din (16.8)