Evaluați adecvarea modelului de regresie:
1. Calculați valorile n de temperatură a apei de la ecuația de regresie y * (x) = ax + b.
2. Construiți un grafic al valorilor calculate Y * și reale y ale temperaturii apei (Figura 3).
3. Calculați varianța modelului y *, care caracterizează variabilitatea liniei de regresie în raport cu valoarea medie,
- Varianța explicată prin ecuația de regresie.
4. Calculați dispersia reziduală. care caracterizează abaterea ecuației de regresie din rezultatele observațiilor y,
5. Calculați coeficientul de determinare prin formula
Coeficientul de determinare arată fracția varianței seriei inițiale, care este descrisă de modelul de regresie.
pentru a trage o concluzie privind abaterea de la liniaritate.
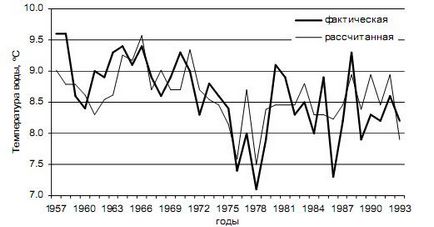
Figura 3 - Actuală și calculată din ecuația valorilor de regresie
6. Evaluați adecvarea modelului de regresie. Pentru a face acest lucru, prezentați ipoteza nulă despre egalitatea de variații
Pentru a le testa, utilizați criteriul F al lui Fisher. Calculați relația de dispersie
care este comparat cu Fable (v1, v2, a) pentru un anumit nivel de semnificație a, a = 0,05 și grade de libertate v1 = 1, v2 = n - 2 (a se vedea tabelul 4 din apendicele 2).
Dacă Fcr> Ftab. atunci ipoteza nulă cu privire la egalitatea de variații este respinsă, ceea ce înseamnă în cazul în cauză caracterul adecvat al modelului de regresie.
7. Analizați calitatea modelului de regresie obținut, având în vedere că pentru un model bun trebuie îndeplinite următoarele condiții:
1) coeficientul de corelare trebuie să fie semnificativ;
2) toți coeficienții de regresie ar trebui să fie semnificativi;
3) modelul trebuie să fie adecvat;
4) coeficientul de determinare ar trebui să fie mai mare de 0,7;
5) eroarea standard a modelului se ar trebui să fie mai mică de 0,67 din deviația standard Sy din seria originală Y.
Un exemplu de calcule este prezentat în Tabelul 2.
Lucrare individuală nr. 2
Construcția unei funcții de autocorelare
Construiește și analizează funcția de autocorelare a celei de-a treia serii de temperatură a apei (notată cu yt.). Pentru a face acest lucru:
1. Calculați funcția de autocorelare rs pentru fiecare schimbare s prin formula
unde T este lungimea implementării, s este schimbarea care se schimbă de la 1 la maxim, de exemplu, smax = 13.
Datorită parității funcției de autocorelare, seriile de timp pot fi mutate în ambele părți (înainte sau înapoi).
2. Construiește un grafic al funcției de autocorelare.
3. Analizați rezultatele. Indicați tipul de proces aleatoriu care caracterizează graficele funcțiilor de autocorelare ("zgomot alb", "zgomot de culoare", ciclicitate etc.).