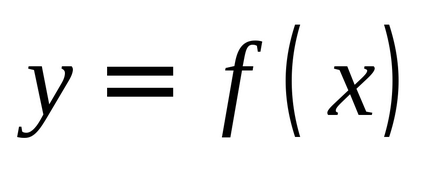§ 8. Principalele caracteristici ale unei funcții numerice 85
8.1. Domeniul de aplicare și domeniul funcției 86
8.2. Funcții zerouri și intervale ale semnului constant 87
8.3. Paritatea, ciudățenia funcțiilor 89
8.4. Periodicitatea funcției 91
8.5. Monotonicitatea și extrema funcției 95
8.6. Valorile cele mai mari și cele mai mici ale funcției 98
8.7. Boundedness a funcției 99
8.8. Exerciții pentru muncă independentă 99
Întrebări pentru auto-examinare 101
Lista caracteristicilor de bază a unei funcții numerice include de obicei:
- domeniul definirii funcției,
- gama de funcții,
- zerouri și intervale de semne ale constanței funcției,
- paritatea, funcția ciudată,
- intervale de monotonie a funcției,
- cele mai mari și cele mai mici valori ale funcției,
Aceste caracteristici sunt adesea numite caracteristici globale ale funcției. deoarece acestea caracterizează funcția numerică ca întreg. În continuare vom studia caracteristicile funcțiilor încă locale - limita, continuitatea, diferențiabilitatea, diferențialul care descriu proprietățile funcțiilor la nivel local, adică în vecinătatea valorilor individuale ale argumentului său. Caracteristicile globale ale unei funcții sunt cunoscute în principal din matematica elementară, deci aici sunt repetate într-o prezentare generală.
Domeniul de aplicare și domeniul de aplicare al funcției
Domeniul funcției numerice (OOF)
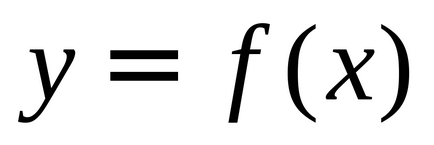
OOF este principala caracteristică a oricărei funcții, luând în considerare toate celelalte caracteristici;
OOF este cel mai des găsit ca un subset X al setului de numere reale
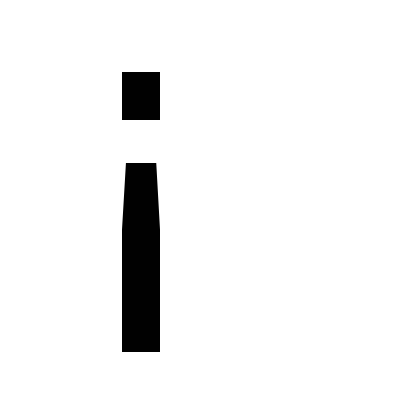
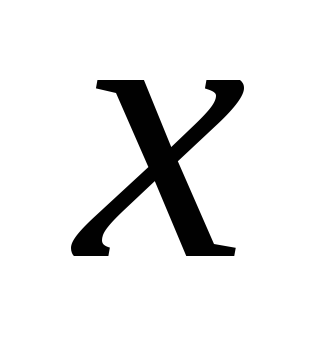
OOF poate fi în sensul unei funcții
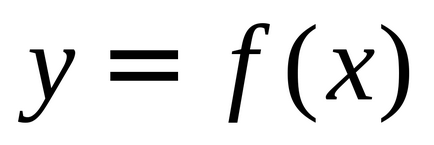
Gama de valori ale unei funcții numerice (OZF)
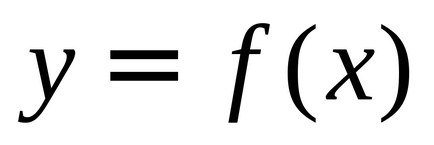
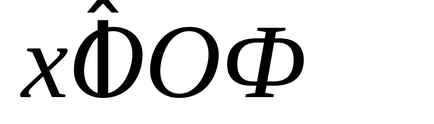
OZF este o caracteristică auxiliară a unei funcții, care este complet determinată după trasarea unui grafic al funcției. Înainte de a construi graficul, un OZF poate fi găsit numai în cazuri individuale, când ajută la a face cunoscute proprietățile funcțiilor elementare de bază prin intermediul cărora se înregistrează funcția studiată. Notația E (f) sau E (y) este, de asemenea, acceptată pentru OZF.
Exemplul 1 (determinarea OOP și OZF)
OZF:
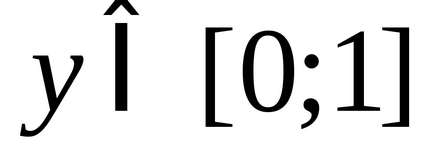
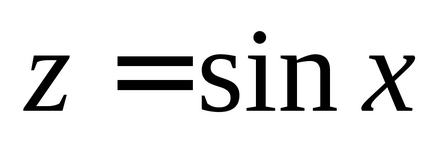
OOF este scris din constrângerea divizării: este imposibil să se împartă cu zero;
OZF poate fi găsit numai după trasarea graficului funcției;
OOF este definită prin operația de extragere a rădăcinii pătrate, care este semnificativă doar pentru numerele nonnegative;
OZF:
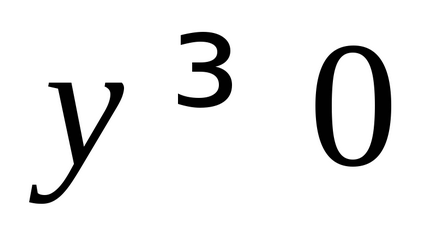
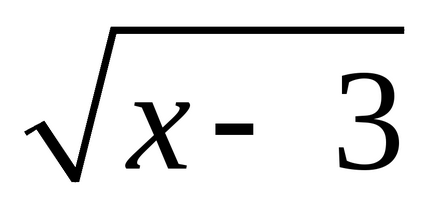
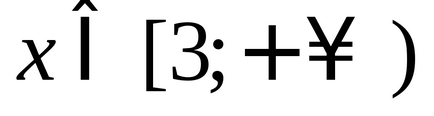
Aici OOF ia în considerare limitările operației logaritmice (logaritmurile există numai din numere pozitive) și operațiunile de divizare (este imposibil să se împartă cu zero);
OZF este determinat după plotarea funcției;
Aici, OOF este scris în funcție de sensul alocării funcției;
OZF:
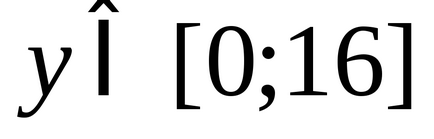
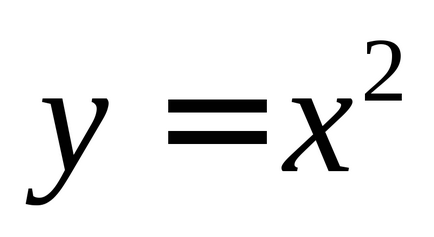
6) o secvență cu un termen comun
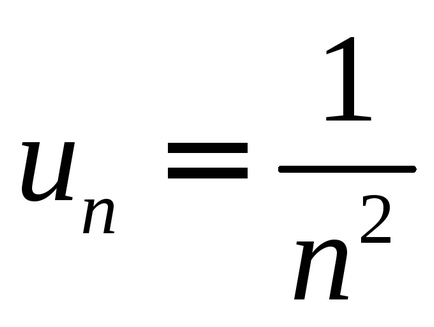
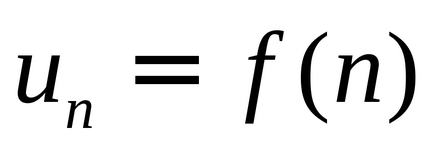
aici este scris OOF în funcție de sensul de atribuire funcție, OZF:
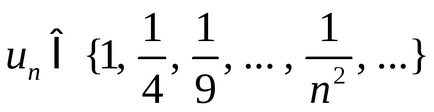
Astfel, ca OOF și OZF