O încercare de a diviza un număr de un vector are ca rezultat un mesaj de eroare:
Dimensiunile matricei trebuie să fie de acord.
Acest lucru se datorează faptului că operația / în MatLab este destinată, în special, rezolvării sistemelor de ecuații algebrice liniare. Dacă doriți să împărțiți un număr în fiecare element al unui vector și să scrieți rezultatul într-un vector nou, utilizați ./
Toate operațiile de mai sus sunt aplicabile atât pentru rândurile vectoriale, cât și pentru coloanele vectoriale.
Construirea unui tabel de valori pentru o funcție
Cartografierea unei funcții într-un format de tabel este convenabilă dacă există un număr relativ mic de valori de funcții. Să fie necesar să se afișeze în fereastra de comandă un tabel cu valorile funcției
puncte 0,2, 0,3, 0,5, 0,8, 1,3, 1,7, 2,5. Problema este rezolvată în două etape.
1. Creați un vector de rând x care conține coordonatele punctelor date.
2. Calculați funcția y (x) din fiecare element al vectorului x și notați valorile obținute în vectorul de rând y. Este important doar să o faceți corect! Este necesar să se găsească valorile funcției pentru fiecare element al vectorului rând x, astfel încât operațiile din expresia funcției trebuie să fie efectuate în funcție de element, așa cum este descris mai sus.
>> x = [0,2 0,3 0,5 0,8 1,3 1,7 2,5]
-1,2978 -0,8473 -0,2980 0,2030 0,8040 1,2258 1,8764
Fiți atenți. că atunci când încearcă să folosească operațiunile de exponentiere, împărțind / multiplicând * (care nu aparțin celor care au un element), un mesaj de eroare este afișat deja când păcatul (x) este pătrat:
> y = sin (x) ^ 2 / (1 + cos (x)) + exp (-x) * log (x)
Matricea trebuie să fie pătrată.
Faptul este că operațiile MatLab * și ^ sunt folosite pentru a multiplica matrici de dimensiuni corespunzătoare și pentru a ridica o matrice pătrată la o putere.
MatLab oferă o creare simplă a vectorilor, fiecare element al cărui element diferă de cel precedent printr-o valoare constantă, adică un pas. Pentru a introduce astfel de vectori, utilizați un colon (nu confundați cu indexarea cu un colon). Următorii doi operatori duc la formarea acelorași vectori de șiruri:
»X = [1, 1,2, 1,4, 1,6, 1,8, 2,0]
În mod condiționat, este posibil să notați
x = [valoarea inițială. pas. valoarea finală]
Nu este necesar să se aibă grijă ca suma valorii penultimate și a pasului să fie egală cu valoarea finală, de exemplu, atunci când se execută următorul operator de atribuire
vectorul rând este umplut cu un element care nu depășește valoarea finală pe care am definit-o. De asemenea, pasul poate fi negativ:
1.9000 1.7000 1.5000 1.3000 1.1000
În cazul unui pas negativ pentru a obține un șir de vector non-gol, valoarea inițială trebuie să fie mai mare decât valoarea finală.
Încercați să umpleți vectorul coloanei cu elemente care încep de la zero și se termină cu incrementări de 0,5 în 0,1. Pentru a face acest lucru, trebuie să specificați vectorul de rând y și apoi să utilizați operația de transpunere:
Rețineți că elementele unui vector plin cu un colon nu pot fi decât reale, astfel încât să puteți folosi un apostrof în locul unui apostrof pentru transpunere.
Un pas egal cu unul este permis să nu se precizeze când se completează automat:
Ieșiți acum tabelul valorilor funcției
pe intervalul [0, 1] în pași de 0,05, efectuând următoarele acțiuni:
3. Formați vectorul de rând x cu un colon.
4. Calculați valorile lui y (x) din elementele x (nu uitați să utilizați multiplicarea elementului).
5. Înregistrați rezultatul în vectorul rândului y.
6. Ieșiri x și y.
Rezultatul afișat pe ecran nu este foarte similar cu tabelul:
Coloanele de la 1 la 7
Coloanele 8 până la 14
0.3500 0.4000 0.4500 0.5000 0.5500 0.6000 0.6500
Coloanele 15 până la 21
0.7000 0.7500 0.8000 0.8500 0.9000 0.9500 1.0000
»y
Coloanele de la 1 la 7
0 0.4560 0.7614 0.8586 0.7445 0.4661 0.1045
Coloanele 8 până la 14
-0.2472 -0.5073 -0.6233 -0.5816 -0.4071 -0.1533 -0.1123
Coloanele 15 până la 21
Linile Vector-x și y constau din douăzeci și unu de elemente, nu se potrivesc pe ecran într-o singură linie și sunt afișate în părți. Deoarece x și y sunt stocate în matrice bidimensionale de dimensiunea unu la douăzeci și unu, ele sunt transmise prin coloane, fiecare dintre ele constituind dintr-un singur element. În primul rând, coloanele sunt scoase de la prima la a șaptea (coloanele i prin 7), apoi - a opta a paisprezecea (coloanele 8 până la 14) și în final - de a cincisprezecea la douăzeci și unu (coloane este prin 21). Mai mult grafic și convenabil este reprezentarea grafică a funcției.
Plotarea unei funcții a unei variabile
MatLab are capabilități grafice bine dezvoltate pentru vizualizarea datelor. În această lucrare de laborator, considerăm construirea celei mai simple grafice a unei funcții a unei variabile prin exemplul unei funcții
definită pe intervalul [0, 1]. Ieșirea funcției de mapare a funcțiilor ca un grafic constă în următorii pași:
· Specificați vectorul valorilor argumentului x.
· Calculul valorilor y ale funcției y (x).
· Apelați comanda plot pentru a compila graficul.
Comenzi pentru a specifica vectorul x și funcții de calcul mai bine finisaj pentru a suprima virgulă ieșirea din fereastra de comandă a valorilor (după virgulă comanda complot pus în mod opțional, t. K. Nu are ieșire nimic la fereastra de comandă). Nu uitați să utilizați multiplicarea elementului
>> y = exp (x). * sin (10 * x);
După executarea comenzilor, numărul ferestrei 1 cu graficul de funcții prezentat în Fig. 2.1. Fereastra conține un meniu, o bară de instrumente și o zonă grafică.
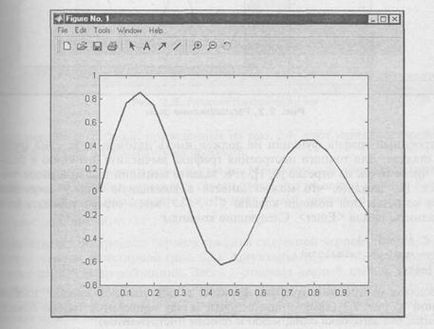
Fig. 2.1. Graficul cel mai simplu al funcției
Pentru a construi un grafic de funcții, doi vectori de aceeași dimensiune, de exemplu x și y, trebuie să fie definiți în mediul de lucru al MatLab. Matricea corespunzătoare x conține valorile argumentelor și y valorile funcției
din aceste argumente. comandă complot conectează punctele cu coordonatele (x (i), y (i)) prin linii drepte, scalarea automat axa pentru amplasarea optimă a graficii în fereastra. Atunci când charting este convenabil situat pe fereastra principală ecran MatLab și fereastra de program de lângă, astfel încât acestea nu se suprapun, așa cum se arată în Fig. 2.2.
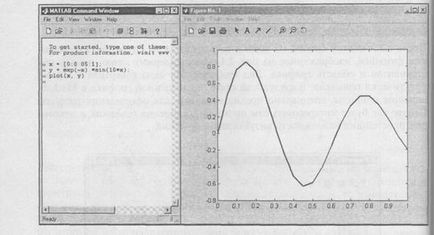
Fig. 2.2. Localizarea ferestrelor
Graficul funcției construite nu trebuie să aibă îndoială, deoarece funcția însăși este netedă. Pentru o plotare corectă a graficului, calculați funcția într-un număr mai mare de puncte din intervalul [0, 1], adică setați un pas mai mic la intrarea în vectorul x. Nu uitați că puteți introduce comenzile introduse în linia de comandă utilizând tastele <↑>, <↓>, Apoi le editați și executați făcând clic pe
conduc la construirea unui grafic al funcției sub forma unei curbe netede, prezentată în Fig. 2.3.
Este convenabil să se compare mai multe funcții prin afișarea graficelor pe o axă. De exemplu, construiți grafice ale funcțiilor pe intervalul [-1, - 0,3]
utilizând secvența de comandă prezentată mai jos:
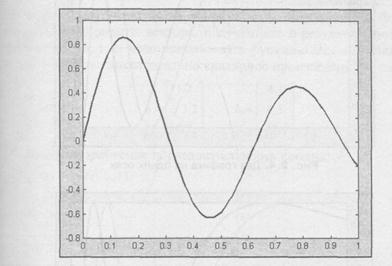
Fig. 2.3. Funcție grafică netedă
Graficele rezultate, prezentate în Fig. 2.4, oferă o reprezentare vizuală a comportamentului funcțiilor studiate.
MatLab afișează grafică în culori diferite. Imprimanta monocrom imprimă grafică în diferite nuanțe de gri, ceea ce nu este întotdeauna convenabil. Comanda complot vă permite să setați cu ușurință stilul și culoarea liniilor, de exemplu
>> grafic (x, f, 'k-', x, g, 'k:')
face construcția primei diagrame o linie neagră solidă, iar cea de-a doua linie neagră punctată (Figura 2.5). Argumentele "k" și "k:" specifică stilul și culoarea primelor și a doua linii. Aici, k înseamnă negru și o cratimă sau colon este o linie solidă sau punctată.
Construcția grafurilor de funcții în MatLab necesită înțelegerea muncii cu vectori - trebuie să aveți posibilitatea să introduceți vectori, să utilizați un colon pentru umplerea tematică cu un anumit pas, să aplicați operații elementale pentru a calcula funcțiile din vectorul valorilor argumentului.