copie
1 11 clasa 11.1 În sistemul mecanic prezentat în figură, o bară cu masa M poate aluneca de-a lungul șinelor fără frecare. În momentul inițial, încărcătura suspendată pe fir este retrasă cu un unghi α și eliberată. Care este masa m a acestei sarcini daca unghiul format de firul cu verticala nu se schimba cand sistemul se misca? Notăm fir modul de elasticitate și rezistență prin modulul de accelerare a barei (a se vedea desenul.) Deoarece unghiul de mișcare a sistemului rămâne constantă, proiecția orizontală a accelerației de sarcină este de asemenea egală. Evident, că este proiecția accelerației și sarcinii pe direcția firului (lungimea firului de schimbare de lungime, situata in spatele blocului, modulul este întotdeauna în mișcare bar). Prin urmare, și (1) în cazul în care masa de marfă. Două forțe de elasticitate a unui fir acționează asupra unui bloc cu un bloc din punctul A. Prin urmare, putem scrie următoarea ecuație pentru bara (în proiecția pe direcția orizontală): (2) Din ecuațiile (1) și (2) obținem: A:
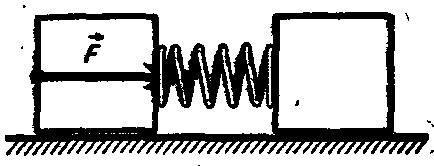
2 11.2 Pe o masă orizontală netedă există câte doi cuburi identice cu masa m fiecare. Cuburile sunt conectate printr-un arc de rigiditate k. Lungimea arcului în stare nedeformată este l 0. Forța F, constantă în valoare absolută și direcție, acționează asupra cubului stâng. Găsiți distanța minimă și maximă între cuburi atunci când sistemul se mișcă. Atunci când distanța dintre cuburi este minimă sau maximă, ambele cuburi se deplasează cu aceeași viteză, iar energia cinetică a sistemului este. În acest caz, energia potențială a sistemului este egală cu energia potențială a arcului comprimat, adică (unde variația în lungimea arcului este considerată pozitivă dacă lungimea arcului este mai mică și negativă dacă lungimea arcului este mai mare). Energia totală a sistemului este egală cu suma energiilor cinetice și potențiale, adică Acest sistem a dobândit această energie prin forța de forță, apoi (1). De unde este distanța pe care cubul stânga (conform figurii) a trecut de momentul în care lungimea primăverii a devenit minimă. Dacă distanța parcursă de centrul de masă al sistemului (vezi figura), atunci () Viteza cuburilor este egală cu viteza centrului de masă al sistemului. Deoarece o forță externă constantă acționează asupra sistemului, centrul de masă se mișcă uniform cu accelerația. Prin urmare, după ce am desemnat timpul de la începutul mișcării până în momentul în care lungimea primăverii a devenit egală, putem scrie: Înlocuind aceste expresii pentru u în ecuația (1), obținem:
3 () De aici sau de aici. Astfel, distanța minimă dintre sarcini este egală cu, și maximul. Răspuns. Două condensatoare identice A și B, cu o capacitate de fiecare C și o bobină cu inductanță L sunt conectate așa cum se arată în figură. La momentul inițial tasta Pentru a deschide, condensatorul A este încărcat la o tensiune U. Condensatorul nu este încărcat, și nu există nici un curent în bobina. Determinați valoarea maximă a curentului în bobină după închiderea cheii. Dacă nu există condensator B, atunci după închiderea cheii în circuit, s-ar produce oscilații electromagnetice. Din legea conservării energiei se poate găsi imediat curentul maxim. Dar în prezența unui condensator B, sarcina va fi redistribuită mai întâi între condensatori și numai atunci oscilațiile vor fi stabilite în circuit. Într-adevăr, segmentul de circuit, format din doi condensatori și fire de conectare, poate fi de asemenea considerat un circuit oscilant. Dar inductivitatea de cabluri inductanță este foarte mică (în comparație cu L), prin urmare, frecvența naturală în acest circuit este foarte mare (mult mai mare decât frecvența de oscilație naturală în circuit, care este format din condensatori și bobina de inducție). Desigur, acest circuit are și o rezistență activă, dar este mic în comparație, de exemplu, cu rezistență inductivă. Prin urmare, pentru o perioadă de timp după închiderea cheii, oscilațiile din circuit pot fi considerate neambalate. În circuitul constând din condensatori și fire, vor exista o mulțime de oscilații curente, în timp ce curentul în bobina poate fi încă considerat egal cu zero. Datorită rezistenței firelor, oscilațiile din acest circuit vor fi amortizate. Aceasta va conduce la o stabilire rapidă a echilibrului și la o redistribuire a tarifelor în mod egal între condensatori (capacitățile de con-
dacă ($ this-> show_pages_images $ page_num doc ['images_node_id'])
4 denseri sunt aceiași). În acest caz, o parte din energia câmpului electric al condensatorului A încărcat intră în energia internă. Să vedem câtă energie rămâne în circuit după o redistribuire rapidă a încărcării între condensatori. Încărcarea inițială a condensatorului A a fost egală cu După redistribuirea sarcinii între condensatori, încărcăturile lor de oțel au fost egale, iar energia. Prin urmare, energia totală care rămâne în circuit este + = Deoarece circuitul cheie înainte ca energia este în bucla a fost apoi trecut în jumătatea interioară a energiei inițiale a condensatorului A. Acum considerăm circuitul format din condensatoare și bobine. Curentul în bobină va fi maxim atunci când condensatoarele sunt complet descărcate și energia lor va intra în energia câmpului magnetic din bobină. Din legea conservării energiei rezultă că de aici. Răspuns: O cavitate termoizolată cu găuri identice este conectată la două volume care conțin gaz heliu. Presiunea de heliu in aceste volume se menține constantă și egală cu P și T temperatura sunt menținute egale într-unul dintre volumele și 2T în cealaltă. Găsiți presiunea și temperatura la starea de echilibru din interiorul cavității. La echilibru, numărul de particule din cavitate trebuie să rămână constant. Acest lucru înseamnă că numărul de particule care în timpul căderii în cavitatea trebuie să fie egal cu numărul de particule emise în această perioadă a cavității. Folosind formula pentru numărul de particule care cad în gaz la
5 zona tampon S, poate fi numărul de particule N, intră în cavitatea, exprimată după cum urmează: în cazul în care valorile concentrației particulelor, respectiv în volumele din stânga și dreapta, și - respectiv valorile medii ale modulelor de proiecție a vitezei particulelor în aceste volume de pe găuri perpendiculare pe axa X. Numărul de particule care în acest timp sunt emise din cavitatea prin gaura suprafață totală 2S, este egal cu n-concentrația particulelor în cavitatea, valoarea medie a modulului de proiecție a particulelor pe axa X. egalând și obține unde proporțional viteză medie pătratică și particule. Prin urmare, putem scrie: Viteza medie a particulelor se determină prin formula: în care m masa a moleculei și temperatura T a gazului, k constanta Boltzmann. Concentrația particulelor poate fi găsit de formula pentru presiunea gazului p: Folosind aceste expresii, obținem: (1) Nici o schimbare în cavitatea și energia totală a particulelor. Aceasta înseamnă că energia adusă de particulele care intră în cavitate este purtată de particulele emise din cavitate. Dar energia medie pe particulă este. În consecință, particulele se încadrează în cavitatea în timpul de timp, energie și să aducă particulele care zboară departe de cavitatea, purtat în această perioadă și egalează energia, obținem: () (2) Rezolvarea ecuației (1) și (2), împreună, vom găsi:
6 Răspuns: 11.5 De ce este mai bine să vedeți un pește care plutește într-un râu de la un pod decât dintr-un mal mic? Atunci când peștele este văzut de pe pod, razele de lumină care vin de pe acesta trec pe suprafața apei aproape perpendiculară pe ea. În același timp, lumina se reflectă nesemnificativ din suprafața apei și, prin urmare, fluxul de lumină provenit din pește este relativ mare. Dacă ne uităm la peștii de la țărmul inferior, razele care vin de la pește la observator formează un unghi mare cu normalul la suprafață și cea mai mare parte a fluxului de lumină reflectă de pe suprafață. În ochii observatorului, în plus, razele soarelui cade, creând un fundal orbitos. Când sunt văzuți de pe pod în ochi, acele raze căderi care au căzut pe suprafața apei și s-au reflectat din ea aproape în unghi drept. Aceste raze se reflectă relativ slab și creează un fundal moale. Dimpotrivă, reflectarea razei care atinge suprafața la un unghi mare este mare, iar lumina soarelui atunci când vizionează peștii de pe țărm creează un fundal luminos care agravează condițiile de observare a peștilor.