Sarcină. Punctele A (2,1), B (1, -2), C (-1,0) sunt vârfurile triunghiului ABC.
a) Gasiti ecuatiile laturilor triunghiului ABC.
b) Gasiti ecuatia unuia dintre medianii triunghiului ABC.
c) Gasiti ecuatia uneia dintre inaltiile triunghiului ABC.
d) Gasiti ecuatia unuia dintre bisectoarele triunghiului ABC.
e) Găsiți zona triunghiului ABC.
Soluția se realizează utilizând un calculator.
Coordonatele triunghiului sunt date: A (2,1), B (1, -2), C (-1,0).
1) Coordonatele vectorilor
Gasim coordonatele vectorilor dupa formula:
X = xj - xi; Y = yj - yi
aici X, Y sunt coordonatele vectorului; xi. yi sunt coordonatele punctului Ai; xj. yj sunt coordonatele punctului Aj
De exemplu, pentru vectorul AB
X = x2 - x1; Y = y2 - y1
X = 1-2 = -1; Y = -2-1 = -3
AB (-1; -3)
AC (-3; -1)
BC (-2; 2)
2) Module de vectori
Lungimea vectorului a (X; Y) este exprimată prin coordonatele sale prin formula:
3) Unghiul dintre liniile drepte
Unghiul dintre vectorii a1 (X1; Y1), a2 (X2; Y2) poate fi găsit prin formula:
unde a1 a2 = X1X2 + Y1Y2
Să găsim unghiul dintre laturile AB și AC
# 947; = arccoși (0,6) = 53,13 °
4) Proiecția vectorului
Proiecția vectorului b pe vectorul a poate fi găsită din formula:
Să găsim proiecția vectorului AB pe vectorul AC
5) Zona triunghiului
Fie ca punctele A1 (x1; y1), A2 (x2; y2), A3 (x3; y3) să fie vârful triunghiului, atunci suprafața sa este exprimată prin formula:
Determinantul de ordinul doi se află în partea dreaptă. Zona triunghiului este întotdeauna pozitivă.
Soluția. Luând A ca primul vârf, găsim:
Prin formula obținem:
6) Divizarea unui interval în acest sens
Vectorul de rază r al punctului A împărțind segmentul AB în raportul AA: AB = m1: m2. este definit de formula:
Coordonatele punctului A sunt date de formulele:
Ecuația mediană a triunghiului
Indicăm mijlocul laturii BC cu litera M. Apoi coordonatele punctului M pot fi găsite din formulele divizării segmentului în jumătate.
M (0; -1)
Gasim ecuatia mediana AM utilizand formula pentru ecuatia unei linii drepte care trece prin doua puncte date. AM median trece prin punctele A (2; 1) și M (0; -1), prin urmare:
sau
sau
y = x-1 sau y-x +1 = 0
7) Ecuația liniei
O linie dreaptă care trece prin punctele A1 (x1; y1) și A2 (x2; y2) este reprezentată prin ecuațiile:
Ecuația liniei AB
sau
sau
y = 3x5 sau y-3x + 5 = 0
Ecuația liniei AC
sau
sau
y = 1/3 x + 1/3 sau 3y-x-1 = 0
Ecuația liniei drepte BC
sau
sau
y = -x-1 sau y + x +1 = 0
8) Lungimea înălțimii triunghiului trasată de la vârful A
Distanța d de la punctul M1 (x1; y1) la linia Ax + By + C = 0 este egală cu valoarea absolută a valorii:
Gasim distanta dintre punctul A (2; 1) si linia BC (y + x +1 = 0)
9) Ecuația de înălțime prin vârful C
Linia dreaptă care trece prin punctul M0 (x0; y0) și perpendiculară pe linia Ax + By + C = 0 are un vector de direcționare (A; B) și, prin urmare, este reprezentată de ecuațiile:
Această ecuație poate fi găsită și într-un alt mod. Pentru aceasta, găsim panta k1 a liniei AB.
Ecuația AB: y = 3x -5, adică k1 = 3
Gasim coeficientul unghial k al perpendicularului din conditia perpendicularitatii a doua linii drepte: k1 * k = -1.
Înlocuind panta liniei date pentru k1, obținem.
3k = -1, unde k = -1 / 3
Deoarece perpendiculul trece prin punctul C (-1,0) și are k = -1 / 3, vom căuta ecuația lui în forma: y-y0 = k (x-x0).
Înlocuind x0 = -1, k = -1 / 3. y0 = 0 obținem:
y-0 = -1 / 3 (x - (-l))
sau
y = -1 / 3 x - 1/3
Ecuația bisectorului unui triunghi
Să găsim bisectorul unghiului A. Se indică punctul de intersecție al bisectorului cu partea BC BC de M.
Folosim formula:
Ecuația AB: y -3x +5 = 0, ecuația AC: 3y -x - 1 = 0
^ A ≈ 53 0
Bisectorul împarte unghiul la jumătate, deci unghiul NAK ≈ 26,5 0
Panta pantei AB este 3 (deoarece y -3x +5 = 0). Unghiul de înclinare este 72
^ NKA≈ 180 0 - 72 0 = 108 0
^ ANK ≈ 180 0 - (108 0 + 26,5 0) ≈ 45,5 0
tg (45,5 °) = 1
Bisectrix trece prin punctul A (2,1), folosind formula, avem:
y - y0 = k (x - x0)
y-1 = 1 (x-2)
sau
y = x-1
Descărcați: xml
Un exemplu. Coordonatele vârfurilor triunghiului ABC sunt date: A (-3; -1); B (4; 6); C (8; -2).
Este necesar: 1) să se calculeze lungimea laterală a aeronavei; 2) alcătuiesc ecuația partidului BC; 3) găsiți unghiul interior al triunghiului la vârful B; 4) să compunem ecuația altitudinii AA, extrasă din vârful A; 5) găsiți coordonatele centrului de greutate al unui triunghi omogen (punctele de intersecție ale medianilor); 6) faceți un desen în sistemul de coordonate.
- compune ecuația mediană trasată de la punctul B și calculați lungimea lui.
- trasează o ecuație pentru înălțimea trasată de la vârful A și își calculează lungimea.
- Găsiți cosinusul colțului interior B al triunghiului ABC.
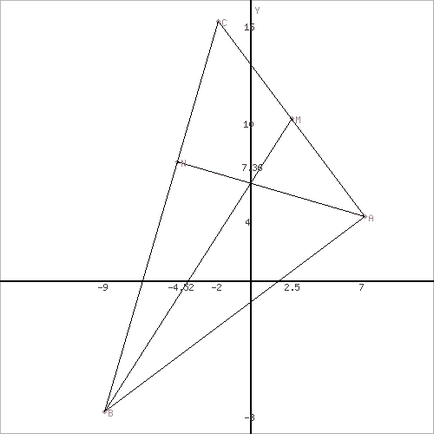
Exemplul №3. Se dau vârfurile A (1; 1); B (7; 4); C (4; 5) ale triunghiului. Găsiți: 1) lungimea laturii AB; 2) unghiul intern A în radiani de până la 0,001. Desenați un desen.
descărcare
Exemplul №4. Se dau vârfurile A (1; 1); B (7; 4); C (4; 5) ale triunghiului. Găsiți: 1) ecuația înălțimii trase prin vârful C; 2) ecuația mediană trasă prin vârful C; 3) punctul de intersecție a înălțimilor triunghiului; 4) lungimea înălțimii a scăzut de la vârful C. Faceți desenul.
descărcare
Exemplul №5. Având în vedere vârfurile triunghiului ABC: A (-5; 0), B (7; -9), C (11; 13). Determinați: 1) lungimea laturii AB; 2) ecuația laturilor AB și AC și coeficienții lor unghiali; 3) zona triunghiului.
Soluția.
Gasim coordonatele vectorilor dupa formula:
X = xj - xi; Y = yj - yi
aici X, Y sunt coordonatele vectorului; xi. yi sunt coordonatele punctului Ai; xj. yj sunt coordonatele punctului Aj
De exemplu, pentru vectorul AB
X = x2 - x1; Y = y2 - y1
X = 7 - (-5) = 12; Y = -9-0 = -9
AB (12; -9), AC (16; 13), BC (4; 22).
Lungimea laturilor triunghiului
Lungimea vectorului a (X; Y) este exprimată prin coordonatele sale prin formula:
Zona triunghiului
Fie ca punctele A1 (x1; y1), A2 (x2; y2), A3 (x3; y3) să fie vârful triunghiului, atunci suprafața sa este exprimată prin formula:
Determinantul de ordinul doi se află în partea dreaptă. Zona triunghiului este întotdeauna pozitivă.
Soluția. Luând A ca primul vârf, găsim:
Prin formula obținem:
Ecuația liniei
O linie dreaptă care trece prin punctele A1 (x1; y1) și A2 (x2; y2) este reprezentată prin ecuațiile:
Ecuația liniei AB
Ecuația canonică a unei linii drepte:
sau
sau
y = -3 / 4 x -15 / 4 sau 4y + 3x + 15 = 0
Coeficientul unghiular al liniei drepte AB este k = -3 / 4
Ecuația liniei AC
sau
sau
y = 13/16 x + 65/16 sau 16y -13x - 65 = 0
Coeficientul unghiular al liniei drepte AB este k = 13/16