Algoritmi tipici pentru procesarea unei matrice bidimensionale în raport cu diagonalele
Dacă numărul de rânduri și coloane într-o matrice bidimensională de identice, astfel se numește o matrice pătrată. Algoritmii tipici pentru matrice pătrate vă permit să procesați o matrice relativ la elementele diagonale. Dependența elementului index dispus pe secundar diagonală determinat cu ușurință atunci când, după repetarea Lectures 1 (linia celulară număr tot mai mare, numărul coloanei scade).
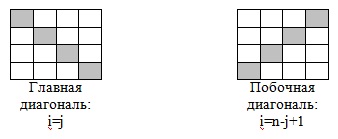
Diagonala principală. Tabelul prezintă algoritmi tipici pentru procesarea elementelor dintr-o matrice bidimensională situată HA, deasupra și sub diagonala principală.
Prelucrarea unei matrici pătrate cu privire la diagonale (by-pass rațional)
Algoritmii tipici menționați mai sus pentru prelucrarea unei matrice pătrate în raport cu diagonalele nu sunt raționale, deoarece toate elementele matricei sunt traversate. Este mai rațional să limităm căutarea elementelor. Rezolva problema introducerii dependenței valorilor inițiale sau finale ale variabilei de control a bucla interioră față de valoarea contorului bucla exterioară.
Să luăm în considerare algoritmi tipici pentru prelucrarea unei matrice pătrate în raport cu diagonalele într-un mod rațional folosind exemple.
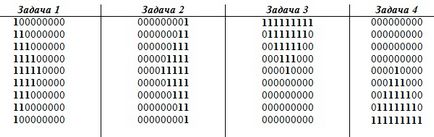
Sarcina: completați elementele matricei pătrate "1" așa cum se arată în imagine:
Mai jos și pe diagonala principală
Deasupra și pe diagonala principală
Deasupra și pe diagonala secundară
Mai jos și pe diagonala secundară
Implementarea de software în BASIC:
Implementarea de software pe Pascal:
Implementarea de software în BASIC:
Implementarea de software pe Pascal:
Implementarea de software în BASIC:
Implementarea de software pe Pascal:
Implementarea de software în BASIC:
Implementarea de software pe Pascal:
Termeni-cheie
- O matrice bidimensională este un set numit de variabile de tip unic, localizat în memorie direct unul lângă celălalt, accesat de index. Arrays cu un index sunt numite unidimensionale, cu două-dimensionale.
- O matrice pătrată este o matrice bidimensională cu același număr de rânduri și coloane.
Rezultatele rezumate
Pentru a rezolva problemele utilizând matrice bidimensionale, este necesar să se utilizeze algoritmi tipici de procesare, cum ar fi:
Procesarea întregii matrice:
- Completare, concluzie
- Sumă, produs
- Elementul maxim (minim)
- Selecție după condiție
Procesarea separată pe rânduri și coloane:
- Completare, concluzie
- Sumă, produs
- Elementul maxim (minim)
- Selecție după condiție
Procesarea în raport cu diagonalele:
- Completare, concluzie
- Sumă, produs
- Elementul maxim (minim)
- Selecție după condiție
Atunci când se procesează o matrice pătrată în raport cu diagonalele acesteia, este necesar să se utilizeze o metodă rațională care exclude traversarea tuturor elementelor matricei.
Setați pentru practică
- Ce se va întâmpla în cazul în care ciclul contorul de swap extern și intern i și ciclurile titlurilor j (în mod obișnuit două dimensiuni-algoritm de procesare matrice)?
- Care este dependența indiciilor elementelor situate pe diagonala principală a unei matrice pătrate? Alături de dvs.?
- Găsiți elementul maxim al șirului minim bidimensional de elemente ale fiecărei linii și elementul minimal al elementelor maximale ale fiecărei coloane din matrice bidimensional de dimensiune n x.
- Umpleți matricele pătrate, așa cum se sugerează în Fig. 5.2.