MI Wexler, G.G. Zegrya
Pentru calcularea capacitanță poate introduce o diferență de potențial între electrozi, pentru a rezolva ecuația Poisson, D găsite pe plăci, iar apoi paramentelor densitate de încărcare de suprafață # 963; = ± Dn (Dn este Dx sau Dr al electrodului). Se presupune că nu există nici un câmp în afara condensatorului (altfel relația # 963; și Dx (r)).
Luați în considerare, de exemplu, simetricul (# 949; = # R49) este un condensator cilindric. În ea
Sarcina. O parte a condensatorului sferic (regiunea # 952;<π/3) заполнена диэлектриком с проницаемостью ε(r) = α/r2, а остальная часть имеет ε(r) = β/r2. Найти емкость, если радиусы обкладок R1 и R2.
Soluția: Schimbarea permeabilității unui dielectric descrisă în problemă poate fi reprezentată ca
(
este o funcție în bucăți care ia valori # 945; și # 946;). Prin urmare, capacitatea poate fi calculată astfel:
Sarcina. În dielectricul de permitivitate # 949; la o distanță de la planul infinit de conducere există o mică minge metalică de rază a<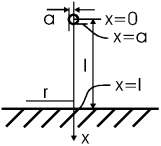
Soluție: Pentru a găsi capacitatea, este necesar, prin specificarea încărcării bilei q, să găsiți diferența de potențial între minge și plan.
Deoarece mingea este foarte mică (a< Diferența potențială poate fi găsită ca unde integritatea este preluată de orice traiectorie care leagă mingea și planul. Desigur, este mai convenabil să se ia cea mai simplă traiectorie: perpendicularul a scăzut de la minge la avion. Introducem axa x de-a lungul acestui perpendicular, astfel încât centrul mingii are o coordonată de 0, iar planul x = l. Metoda imaginii este utilizată pentru a găsi câmpul sistemului. Pe axa x, obținem:Articole similare