Diviziunea este definită ca acțiunea opusă multiplicării. Un număr complex particular z1 și z2 ≠ 0 este numit complexul z, care, atunci când este înmulțit cu z2. dă numărul z1. adică z1 / z2 = z dacă z2 z = z1.
Rezolvând sistemul, găsim valorile lui x și y:
În practică, coeficientul a două numere complexe se găsește prin înmulțirea numărătorului și a numitorului cu numărul conjugat cu numitorul ("a scăpa de imaginar în numitor").
P.2.5 Eliminarea rădăcinilor din numere complexe Extragerea rădăcină a puterii n este definită ca acțiunea opusă ridicării la gradul natural.
Gradul zeros al numărului complex z este numărul complex ω care satisface egalitatea ω n = z, adică dacă ω n = z.
Dacă setăm z = r (cosφ + isinφ) și ω = r (cosθ + isinθ), atunci, prin definiția formula rădăcină și Moivre, obținem
Z = ωn = rn (cos n θ + isin n θ) -r (cosφ + isinφ).
Prin urmare, avem r n = r, nθ = φ + 2πk, k = 0, -1,1, -2,2. Să mănânce
și (rădăcină aritmetică).
Prin urmare, egalitatea ia forma
Obținem n valori diferite ale rădăcinii. Pentru alte valori ale lui k, datorită periodicității cosinusului și sinusului, se obțin valorile rădăcinilor care coincid cu cele deja găsite. Astfel, pentru k = n avem
Astfel, pentru orice z ≠ 0, a n-a rădăcină a z are exact n valori distincte.
Scrieți numerele complexe z1 = -1 + i și z2 = -1 în forme trigonometrice și exponențiale.
Soluție: Pentru z1 avem
adică, j = p. Prin urmare, -1 = cosπ + isinπ = e iπ.
Soluție: Mai întâi, scrieți numărul în forma trigonometrică:
Prin formula Moivre avem
Pentru forma trigonometrică a unui număr complex, formula de fisiune are forma
Atunci când se împart numere complexe, modulele lor, respectiv, sunt împărțite, iar argumentele, respectiv, sunt scăzute.
Soluția: a) Scrieți radicandul într-o formă trigonometrică:
.
b) Noi scriem din nou radicandul in forma trigonometrica:
-1 = Cosπ + isinπ.
Pentru k = 0, obținem ω0 = cos / 2 + isin / 2 = i și pentru k = 1 obținem
Soluția. Acționăm atât asupra polinomilor
Construiți pe planul complex și prezentați în forme trigonometrice și exponențiale următoarele numere complexe:
1) 2) 3) 4) 5).
Soluția. Mai întâi construim toate aceste puncte în planul complex
Acum, să le imaginăm în forme trigonometrice și exponențiale:
Din trimestrul al doilea, atunci
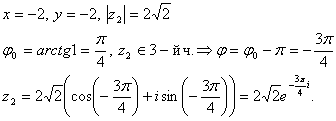
Prezentați în numere de formă exponențială:
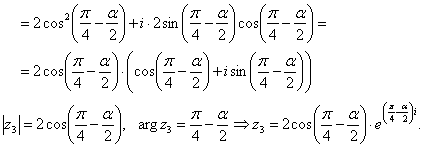
1) Să reprezentăm numărul în forma trigonometrică
Folosind formula Muavre, primim:
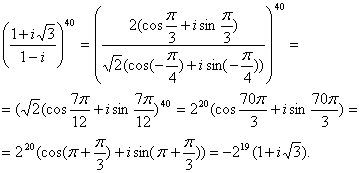
Construiți un grafic de funcții.
Această funcție are forma. adică o funcție uniformă și, în consecință, graficul său este simetric față de axa OY.
Având în vedere acest lucru. atunci este necesar să se construiască un grafic al funcțiilor prin deplasarea de-a lungul axei OX cu 4 unități ale graficului de funcții.
1) ne comparăm funcția (figura 11a);
2) prin deplasarea lui cu 4 unități de-a lungul axei OX, am complotat funcția (Fig.11b);
3) salvăm partea dreaptă (pentru) graficul funcției și afișăm-o simetric pe axa OY. Pentru a clarifica graficul, definim punctul de intersecție al graficului cu axa OY. Când. și anume punctul de intersecție al graficului cu axa OY: (0; -2). Graficul grafic al funcției este prezentat în Fig.
Construiți un grafic de funcții.
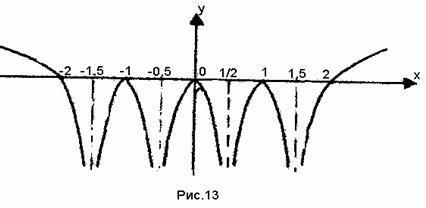
Deoarece, atunci funcția este uniformă și graficul său este simetric față de axa OY. Valorile lui x. sub care expresia sub semnul logaritmului dispare, sunt inadmisibile pentru x și în același timp ajută la găsirea asimptotelor verticale. Să le găsim.
.
Graficul are patru asimptote verticale
.
Definiți zerourile funcției. Avem:
.
Deci, pe axa OX există cinci puncte ale graficului funcției:
(2; 0); (-1; 0); (0; 0); (1; 0); (2; 0). Graficul funcțiilor are patru asimptote. Pentru a compila graficul, este necesar să știm din ce direcție ramurile graficului se apropie de asimptote. Pentru a face acest lucru, este suficient să se determine intervalele semnului constanței funcției. Amintiți-vă că
.
Deci, dacă. atunci y> 0 și, în consecință, dacă și. atunci. Prin urmare, graficul funcției în interval