1 Construirea tabelelor de adevăr într-o foaie de calcul Excel

2 Obiectivele lecției: generalizarea și sistematizarea cunoștințelor pe temele "Tabele de adevăr", "Transformarea expresiilor logice", "Rezolvarea problemelor logice"; formarea abilității de a automatiza soluția sarcinilor logice în foile de calcul MS Excel.

3 Verificarea temelor: Circles Euler - Venn: 66, 67; Metoda tabulară pentru rezolvarea problemelor logice: 59, 127.

4 Inversiunea - o negare logică Din latină. inversio - inversată Negarea logică face falsa exprimare falsă și, dimpotrivă, falsă - adevărată. AF = A Tabelul de adevăr al funcției de negare logică Tradus în limbaj natural: "Nu A" "Nu este adevărat că A" TRUE - 1 FALSE - 0

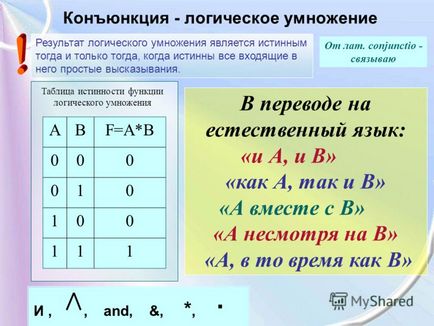
5 Conjuncție - multiplicare logică Din latină. conjunctio - connect Rezultatul multiplicării logice este adevărat dacă și numai dacă toate propozițiile simple incluse în ea sunt adevărate. Tabelul de adevăr al funcției de multiplicare logică ABF = A * B Tradus în limbajul uman, „A și B“ „A și B“ „A, împreună cu B«»Și în ciuda B“ „A în timp ce În I. și, , *, ·
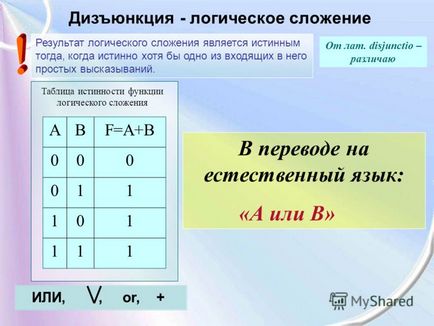
6 Disjuncție - adăugare logică Din latină. disjunctio - disting Rezultatul adăugării logice este adevărat atunci când cel puțin una dintre propozițiile simple incluse în ea este adevărată. Traducere în limbaj natural: "A sau B" Tabelul de adevăr al funcției de adăugare logică ABF = A + B OR. sau, +
7 Implicare - urmări logice Rezultatul unei secvențe logice este fals dacă și numai dacă adevărul este fals. Din lat. IMPLICAȚIILE - îndeaproape asociat tabelul de adevăr de logică funcția inferență ABF = AB A - o condiție în - consecință, tradus în limbaj natural: "dacă A, atunci B", "B, dacă A" "Când A, atunci B", „A suficientă pentru a B "" Dar numai atunci când B "" Pentru A este necesar ca B "

8 Echivalența este o egalitate logică Rezultatul unei egalități logice este adevărat dacă și numai dacă ambele afirmații sunt fie adevărate sau false în același timp. Din lat. aeguivalens - tabel de adevăr echivalent al funcțiilor logice ale egalității ABF = A B tradus în limbajul uman: „A este echivalent cu B“ „A dacă și numai dacă = B“.

9 În limbajul natural al logicii ... și ... ... și ... nu este adevărat că ... ... dacă și numai dacă ... ... dacă ... atunci ... ... dacă și numai dacă ... ... eu nu ... Tabelul de mai jos prezintă, în partea stângă a coloana care conține principalele (legături) logice, cu ajutorul cărora sunt construite într-o declarație complexă limbaj natural. Completați coloana din dreapta a tabelului cu numele corespunzător al operațiilor logice.
10 În limbajul natural În logică. și. coroborat. sau. disjuncție Nu este adevărat acest lucru. negare. totuși. coroborat. în acest caz și numai în acel caz. echivalență. dar. coroborat. a. conjuncție Dacă. atunci. implicație. cu toate acestea. coroborat. dacă și numai dacă. echivalență Fie fie. disjuncție strictă. necesare și suficiente. echivalența dintre. urmează. implicație. atrage după sine. implicație. este echivalentă. echivalență. este necesar. implicație. suficient. implicare înapoi
11 Algoritmul pentru construirea unui tabel de adevăr: 1. Calculați numărul de variabile n într-o expresie logică; 2. Se determină numărul de rânduri în tabel, care este de 2 n numărul 3.Podschitat de operații logice de expresie Boolean și pentru a determina numărul m de coloane din tabel, care este egal cu m + n 4.Vvesti numele coloanelor tabel în conformitate cu secvența logică a performanței operațiilor cu suporturile și prioritățile; 5. Completați coloanele variabilelor de intrare cu seturi de valori; 6. Pentru a umple tabelul de adevăr pe coloane, efectuând operații logice în conformitate cu secvența stabilită în clauza 4.
12 Construirea tabelelor de adevăr într-o foaie de calcul Excel.
14 Scrieți o tabelă de adevăr pentru expresia logică A (V7S).
15 ABSS (B 7 C) A (B7C)
16 Creați o tabelă de adevăr pentru expresia logică din notebook: F = (A7B) (A7S) (VS) Și F = A B v A B F = A (B B C) F = A (B C) F = (A B) v (A B) F = A (B v B C)
17 Tema: 1 (46). Discutând despre construirea unei noi aeronave trohmotornogo, trei designeri la rândul lor, au făcut următoarele ipoteze: 1) eșecul celui de al doilea motor terenului necesar, iar în caz de eșec al treilea, puteți continua zborul; 2) dacă primul motor eșuează, poți zbura sau dacă al treilea motor nu reușește, nu poți zbura; 3) dacă al treilea motor eșuează, poți zbura, dar dacă refuzi cel puțin unul din celelalte, ar trebui să stai jos. Testele de zbor au confirmat corectitudinea fiecărui proiectant. Determinați dacă un motor nu reușește să continue să zboare. 2 (54). Imaginați-vă această situație: pe televizor, meteorologul anunță prognoza meteo pentru ziua de mâine și precizează următoarele: 1. Dacă nu există vânt, va fi vremea tulbure fără ploaie. 2. Dacă plouă, va fi tulbure și fără vânt. 3. Dacă vremea este tulbure, va ploua și nu va mai fi vânt. Deci, ce va fi vremea ca mâine? Nivelul de cunoștințe: Înregistrați starea sarcinilor 1 și 2 în limba algebră a logicii. Dezasambla soluționarea problemelor din manual (f) înțelegerea nivelului: + Pentru a formula avantajele și dezavantajele metodei de rezolvare a problemelor bazate pe algebra logicii. Nivelul de aplicare: + Formulează tipul de sarcini logice rezolvate prin această metodă.