pagina 1
Testarea 7
Legea distribuției normale. Probabilitatea unei cantități aleatorii distribuite în mod normal (LHSV) care se încadrează într-un interval dat.
Informații de bază din teorie.
Distribuția probabilității variabilei aleatoare (CB) X se numește normal dacă densitatea distribuției este definită prin ecuația:
, unde a este așteptarea matematică a CB X; - deviația standard.
Graficul este simetric față de linia verticală. Cu cat este mai mare, cu atat este mai mare magnitudinea curbei. Valorile funcției sunt disponibile în tabele.
Probabilitatea ca CB X să ia o valoare care aparține intervalului: unde este funcția Laplace. Funcția este definită de tabele.
Atunci când = 0, curba este simetrică față de axa OY - aceasta este distribuția standard (sau normalizată) normală.
Deoarece funcția de densitate a probabilității LEL este simetrică în raport cu așteptările matematice, este posibil să se construiască o așa-numită scară de dispersie:
Se poate observa că, cu o probabilitate de 0.9973, se poate argumenta că LDCW va lua valori în intervalul respectiv. Această afirmație a primit în teoria probabilității numele "Regulile celor trei Sigma".
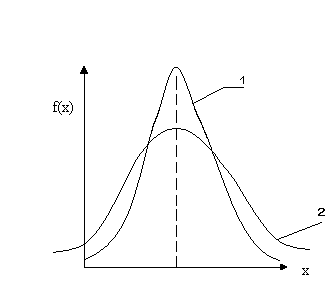
1. Comparați valorile pentru cele două curbe HPC.
2. Variabila aleatoare continuă X este dată de densitatea de distribuție a probabilității. Apoi, așteptarea matematică a acestei variabile aleatoare distribuite în mod normal este:
3. HPLC X este dat de densitatea de distribuție :.
Asteptarile si variatiile matematice ale acestui CB sunt aceleasi:
= 25 = 1 = 25
4. Regula de trei sigma înseamnă că:
1) probabilitatea ca CB să cade într-un interval, adică aproape de unitate;
2) țările cel mai puțin dezvoltate nu pot depăși acest obiectiv;
3) Graficul densității LEL este simetric în raport cu așteptările matematice
5. CB X este distribuit în mod normal cu o așteptare matematică egală cu 5 și RMS, egală cu 2 unități. Expresia pentru densitatea de distribuție a acestui LDCW este:
6. Asteptarile matematice si RMS ale LRSV X sunt egale cu 10 si 2. Probabilitatea ca, ca rezultat al testului CB X, sa ia valoarea cuprinsa in intervalul [9; 11] este:
1) 0,1915 2) 0,3830 3) 0,6211
7. O parte este considerată potrivită dacă deviația X a mărimii reale față de mărimea desenului este mai mică de 0,7 mm în valoare absolută. Abaterile lui X de la mărimea în desen sunt LDCW cu o valoare de = 0,4 mm. Sunt produse 100 de articole; de la ei vor fi:
8. Asteptarile matematice si RMS ale LRSV X sunt egale cu 10 si 2. Probabilitatea ca, ca rezultat al testului CB X, va lua valoarea inchisa in intervalul [12; 14] este:
1) 0,1359 2) 0,8641 3) 0,432
9. Eroarea X a piesei de prelucrat este LDCW cu valoarea a = 10 și = 0.1. Apoi, cu o probabilitate de 0.9973, intervalul dimensiunilor părților, simetric față de a = 10, va fi:
1) 9,7; 10,3 (2) 9,8; 10,2 (3) 9,9; 10.1
10. Cântăriți toate produsele fără erori sistematice. Erorile aleatorii X măsurătorile fac obiectul legii normale cu o valoare de = 10 g. Probabilitatea ca cântărirea să fie efectuată cu o eroare care nu depășește 15 g în valoare absolută este:
1) 0,8664 2) 0,1336 3) 0,4332
11. HPBB X are o așteptare matematică a = 10 și o RMS = 5. Cu probabilitatea 0.9973, valoarea lui X se încadrează în intervalul:
1) (5; 15) 2) (0; 20) 3) (-5; 25)
12. HPBB X are o așteptare matematică a = 10. Se știe că probabilitatea de lovire a lui X în intervalul [10; 20] este egal cu 0,3. Atunci probabilitatea de a obține CB X în intervalul [0; 10] va fi:
13. LRSV X are o așteptare matematică a = 25. Probabilitatea de lovire a X în intervalul [10; 15] este egal cu 0,2. Apoi, probabilitatea de a lovi X în intervalul [35, 40] va fi:
14. Temperatura camerei este menținută de încălzitor și are o distribuție normală cu și. Probabilitatea ca temperatura din această cameră să se situeze în intervalul de până la:
1) 0,95 2) 0,83 3) 0,67
15. Pentru o distribuție normală standard, valoarea este:
16. O distribuție empirică normală se formează atunci când:
1) există un număr mare de cauze aleatorii independente care au aproximativ aceeași greutate statistică;
2) există un număr mare de variabile aleatorii foarte dependente;
3) dimensiunea eșantionului este mică.
Valoarea determină amplitudinea curbei densității de distribuție în raport cu așteptarea matematică. Pentru curba 2, intervalul este mai mare, adică