:
.
Forțele de inerție ale blocului 2 care se rotesc în jurul unei axe fixe cu accelerație unghiulară e2 sunt reduse la o pereche a cărui moment
Forțele de inerție ale patinoarului 3, care efectuează o mișcare plană, sunt reduse la forță
,
- accelerarea centrului de masă al rolei 3 și unei perechi de forțe, momentul căruia
,
unde e3 este accelerația unghiulară a rolei 3, J3 este momentul de inerție al rolei 3 față de axa longitudinală centrală:
.
Informăm sistemul despre posibila mișcare în direcția mișcării sale efective (figura 2). Să facem ecuația generală de dinamică:
unde dj2 și dj3 sunt unghiurile de rotație ale blocurilor 2 și 3.
Având în vedere că G1 = G2 = G = mg, G3 = 3G = 3 mg
Setați relația dintre deplasabil incluse în (1) și între acceleratiile (2), folosind faptul că aceste curbe sunt aceleași ca și între vitezele respective:
dj2 = dj3 = ds1 / R = ds1 / 2r;
ds3 = dj2r = ds1 / 2; (3)
e2 = e3 = a1 / 2r; a3 = a1 / 2.
Având în vedere (2) și (3), ecuația (1), după împărțirea tuturor termenilor lui cu m și ds1, ia forma
,
a3 = a1 / 2 = 1,87 m / s2.
Pentru a determina tensiunea din filament 2-3 taie mental firul și să înlocuiască acțiunea pe rola 3 reacția T2-3 (fig. 3).
Ecuația generală a dinamicii:
,
Pentru a găsi tensiunea din filament 1-2 taie mental firul și să înlocuiască acțiunea pe bunuri 1 prin reacția T1-2 (Fig. 4).
Fără a forma o ecuație generală a dinamicii, pe baza principiului d'Alembert, avem:
Atributul K-3. Determinarea vitezelor și accelerațiilor punctelor unui corp rigid în mișcare plană.
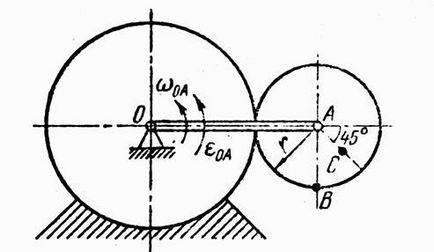
Găsiți pentru o poziție dată mecanismul de viteză și accelerare a punctelor B și C. Schema mecanismului este prezentată în Fig. 1, datele necesare pentru calcul sunt prezentate în tabelul 1.
Datele inițiale în cm și cu:
x = -2t2 + 3; y = -5t; (1)
Ecuațiile de mișcare (1) sunt ecuațiile parametrice ale traiectoriei M. Pentru a obține ecuația traiectoriei într-o formă convențională de coordonate, eliminând timpul t din ecuațiile de mișcare. atunci
Aceasta este ecuația parabolică.
Pentru a determina viteza unui punct, găsim proiecțiile de viteză pe axele de coordonate:
Vx = x '= -4t cm / s; Vy = y '= -5 cm / s.
Modul de viteză a punctului
Similar cu proiecția punctului de accelerare
ax = x "= -4 cm / s2; ay = y "= 0.
Modul de accelerare a punctului
Accelerarea tangențială se găsește prin diferențierea modulului de viteză (3)
x = -2 x 0,52 + 3 = 2,5 cm, y = -5 x 0,5 = -2,5 cm.
Vx = -4 x 0,5 = -2 cm / s, Vy = -5 cm / s, V = 5,38 cm / s.
ax = -4 cm / s2, ay = 0, a = 4 cm / s2
Modulul de accelerare tangențială
Semnul "+" pentru dV / dt arată că mișcarea punctului este accelerată și, prin urmare, direcția
Punct de accelerare normal:
Raza de curbură a traiectoriei în punctul în care pentru t = 0,5 s există un punct M:
Folosind ecuația (2), construim traiectoria (Fig. 1) și arată-l pe poziția unui punct M la un moment predeterminat. vector
construim pe componente
, și este îndreptată de-a lungul tangentei la traiectoria punctului. vector
am găsit atât în ceea ce privește
.