Bazele fizicii solide
Dorind să-și facă compozițiile mai distractive, ei [scriitorii] tratează cititorul cu cele mai mari fabricări ".
Jonathan Swift "Călătoriile lui Gulliver"
Suprafața Fermi nu este o suprafață reală, ci doar o ilustrare grafică a comportamentului electronilor în metale! Imaginile suprafețelor Fermi explică astfel de proprietăți ale metalelor, cum ar fi luciul, ductilitatea, conductivitatea electrică și conductivitatea termică. Metalul în sine poate fi definit ca un corp solid cu o suprafață Fermi.
Din punct de vedere fizic, suprafața Fermi este definită ca suprafața energiei constante a electronului ε F în k-spațiu de impuls.
Bazele fizicii solide
Simetria de translație impune caracteristicile sale pe suprafața Fermi chiar și în cazul în care considerăm că potențialul ionic este zero. Pentru claritate, luați în considerare exemplul bidimensional.
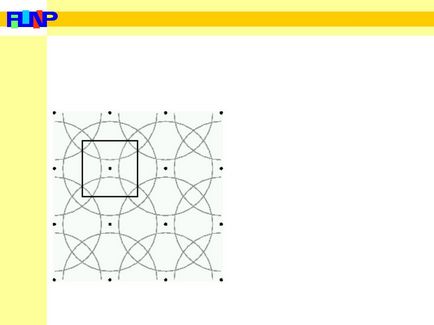
Liniile neregulate prezintă primele trei zone Brillouin ale unei laturi pătrată (zonele de plasă sunt marcate cu puncte negre). Cercul albastru corespunde unei suprafețe de energie constantă pentru electronii liberi
(suprafața Fermi în cazul bidimensional) a unei anumite concentrații.
Bazele fizicii solide
Cu toate acestea, într-o astfel de schemă de zone extinse, suprafața Fermi are discontinuități și imaginea nu este clară
Să desenăm acum suprafețe Fermi bidimensionale lângă fiecare dintre nodurile rețelei reciproce. Pătratul negru arată prima zonă Brillouin. Fiecare punct din spațiul k care cade în cel puțin una din cercuri corespunde stărilor electronice umplute din prima zonă Brillouin. Punctele care se încadrează simultan în două cercuri corespund stărilor pline în a doua zonă Brillouin, simultan în a treia și a treia, și așa mai departe.
Bazele fizicii solide
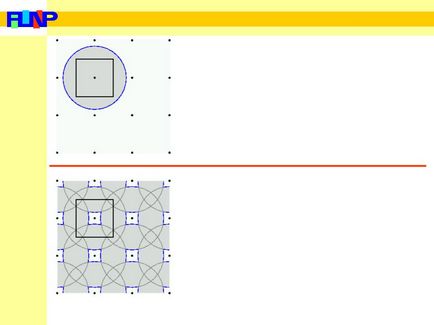
Deci, avem următoarea imagine. Pătratul negru din figură este prima zonă Brillouin. Cercul albastru este suprafața Fermi. Zona gri este ocupată de stări electronice. Astfel, în exemplul nostru, prima zonă este complet umplută.
Trecem în a doua zonă. Pătratul negru este din nou prima zonă Brillouin. Liniile albastre sunt suprafața Fermi pentru a doua zonă Brillouin. Culoarea gri prezintă stadiile electronice umplute în a doua zonă Brillouin.

Bazele fizicii solide
Acum ne îndreptăm spre cazul în care potențialul nucleului ionic nu este zero, dar este suficient de slab pentru a folosi teoria perturbării. În cazul unidimensional, am văzut deja că un potențial periodic slab conduce la efectele de difracție electronică în apropierea limitelor zonei Brillouin și la apariția unor lacune în spectrul energetic al electronilor. Acesta este exact cazul cazului bidimensional examinat.
Pentru a ne imagina calitativ modul în care suprafața Fermi este modificată din cauza potențialului slab al rețelei cristaline, trebuie să ne amintim trei reguli:
1. Suprafața Fermi traversează limita zonelor Brillouin perpendicular pe suprafața benzilor
2. Suprafața Fermi nu se poate schimba în mod continuu când trece prin limita benzilor, deoarece aceasta ar implica faptul că energia electronilor din zonele învecinate din apropierea limitelor lor este diferită. Adică, de-a lungul granițelor zonelor trebuie să existe un salt al valorii vectorului de unde al electronilor.
3. Pentru aceeași valoare a vectorului de undă │ k │, energia electronilor din prima zonă este mai mică decât energia electronilor din a doua zonă și așa mai departe. Ca urmare, electronii curg din a doua zonă la prima, dar în același timp
suprafața (volumul în cazul tridimensional) al suprafeței Fermi este conservată.
Bazele fizicii solide
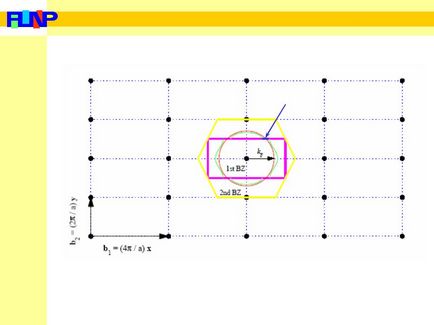
Având în vedere aceste reguli, obținem o imagine a suprafeței Fermi deformată datorită potențialului laturii.
Un salt al valorii vectorului de undă
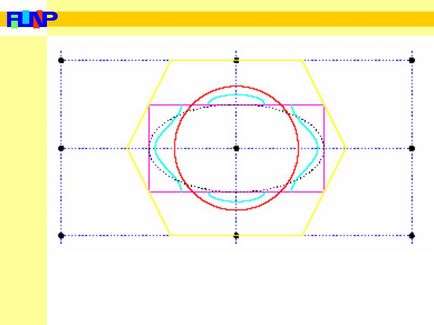
În figură, prima și a doua zonă Brillouin a reticulului reciproc dreptunghiular sunt prezentate în culoarea purpuriu și galben. Cercul roșu este suprafața Fermi pentru electronii liberi și este afișată culoarea verde
Cursul nr. 4 este o suprafață Fermi distorsionată de un potențial de zăbrele slab.
Bazele fizicii solide
Deci imaginea va arăta ca în schema zonelor periodice. În stânga este suprafața Fermi pentru prima zonă Brillouin, spre dreapta pentru a doua. Culoarea gri prezintă stările electronice umplute.
Creșterea potențialului zăbrelei duce la faptul că tot mai mulți electroni tind să curgă în prima zonă Brillouin. Ca rezultat, volumul Fermi al suprafeței din prima zonă crește datorită scăderii acesteia în a doua. Cu un potențial cristalin suficient de puternic, toți electronii vor fi în prima zonă Brillouin (linia gri punctată în figură).