Semnificația geometrică și economică a unui integral integrat

Din definiția rezultă că pentru o funcție nonnegativă f (x) integrale definită

este egal cu aria trapezului curbilinar delimitată de curba y = f (x), liniile drepte x = a, x = b și axa abscisă = 0 (figura 4.1).

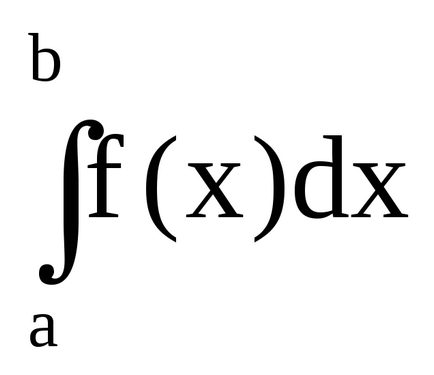
Dacă funcția -f (x) este non-pozitivă, atunci integritatea definită

este egală cu aria trapezului curbilinar corespunzător, luată cu un semn minus (figura 4.7).

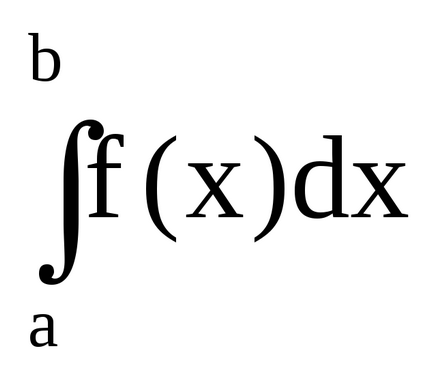
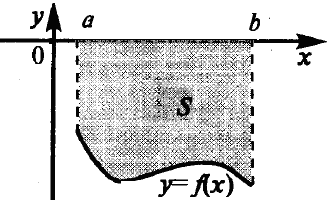
Figura 4.7 - Semnificația geometrică a unui integral integrat pentru o funcție non-pozitivă

Pentru o functie continua arbitrara f (x), integrala definita

Este egal cu suma ariilor trapez curbilinie, situată sub funcția graficului f (x) și deasupra axei orizontale, minus suma pătratelor trapez curbiliniu situată deasupra funcției graficului f (x) și sub axa orizontală (figura 4.8).

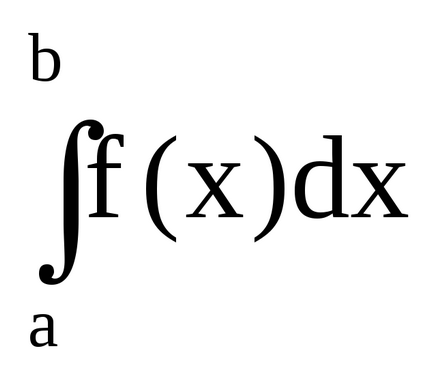
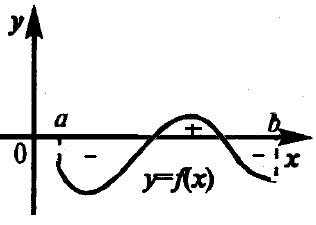
Figura 4.8 - Semnificația geometrică a unui integrat definit pentru o funcție continuă arbitrară f (x) (semnul "plus" este marcat de zona care este adăugată și "minus" este cea care este scăzută).

Atunci când se calculează în practică zonele cu cifre curbiliniare, se folosește deseori următoarea formulă:

, gdeS- figura zonă delimitată între curbele y = f1 (x) și y = f2 (x) pe [a, b], și f1 (x) și f2 (x) - o funcție continuă definită pe acest segment astfel f1 (x) ≥ f2 (x) (vezi figurile 4.9, 4.10).

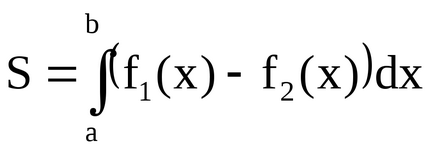
Atunci când studiem semnificația economică a derivatului, sa clarificat că derivatul acționează ca rata de schimbare a unui obiect sau proces economic în timp sau relativ la un alt factor investigat. Pentru a stabili sensul economic al unui anumit integral, este necesar ca această viteză să fie considerată ca o funcție a timpului sau a altui factor. Apoi, intrucat un integrala definita reprezinta o schimbare a antiderivativei, descoperim ca in economie el estimeaza schimbarea acestui obiect (proces) pe o anumita perioada de timp (sau cu o anumita schimbare a altui factor).

De exemplu, dacă funcția q = q (t) descrie productivitatea muncii ca o funcție a timpului, atunci integrarea definitivă a acestei funcții

reprezintă volumul de ieșire dintr-o perioadă de timp de la to0 tot1.

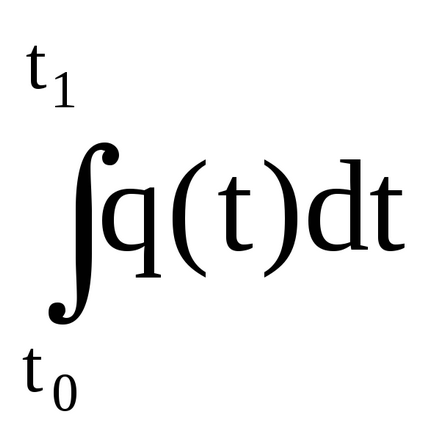
Metodele de calcul pentru integrale definite se bazează pe metodele de integrare discutate anterior (nu vom efectua dovezi).

Când găsirea indefinit integrală, am utilizat metoda de schimbare a variabilei pe baza formulei: f (x) dx = = f ( (t)) ` (t) dt, unde x =  (t) - funcția derivabila prezent interval. Pentru un integral integrat, formula pentru schimbarea unei variabile ia forma

, unde pentru toți.

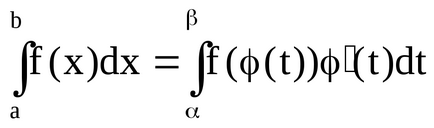
Fie t = 2-x 2. Apoi, dt = -2xdx și xdx = - 1 dt.

Atunci când x = 0, t = 2 - 0 2 = 2. Pentru x = 1t = 2 - 1 2 = 1. Apoi

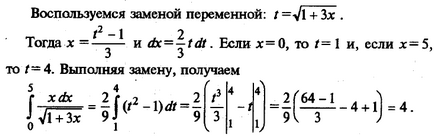
Formula pentru integrarea prin componente pentru un integrat definit ia forma:

, în cazul în care.

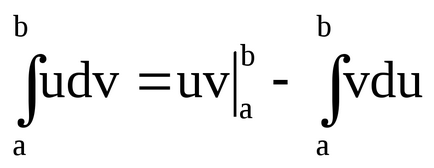
Să presupunem că u = ln (1 + x), dv = dx. atunci

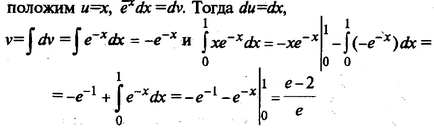
Calcularea ariilor de figuri plane cu ajutorul unui integral integrat

Exemplul 1. Găsiți aria unei figuri delimitată de liniile y = x 2 - 2 și y = x.

Graficul grafic al funcției y = x 2 - 2 este o parabolă cu un punct minim la x = 0, y = -2; axa abscisei se intersectează în puncte

. Graficul grafic al funcției y = x este o linie dreaptă, bisectorul unui trimestru de coordonate nonnegative.

Să găsim coordonatele punctelor de intersecție a parabolei y = x 2 - 2 și linia dreaptă y = x, rezolvând sistemul acestor ecuații:

x = 2; y = 2 sau x = -1; y = -1

Astfel, figura, a cărei suprafață trebuie să fie găsită, poate fi reprezentată în Figura 4.9.

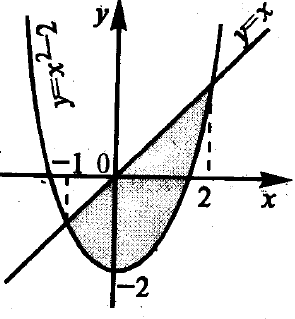
Figura 4.9 - Figura delimitată de liniile y = x 2 - 2 și y = x

Pe intervalul [-1, 2] x ≥ x 2 - 2.

Folosim formula

, setarea f1 (x) = x; f2 (x) = x2-2, a = -1, b = 2.

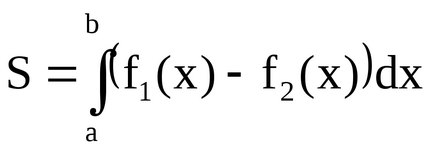
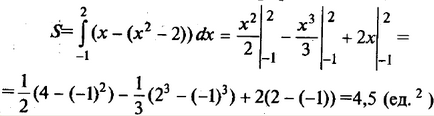
Exemplul 2. Găsiți zona figurului delimitată de liniile y = 4 - x 2 și y = x 2 - 2x.

Graficul grafic al funcției y = 4 - x 2 este o parabolă cu un punct maxim la x = 0, y = 4; axa abscisă intersectează la punctele 2 și -2. Graficul grafic al funcției y = x 2 este o parabolă 2x cu un punct minim la 2x - 2 = 0, x = 1; y = -1; axa abscisă intersectează la punctele 0 și 2.

Să găsim coordonatele punctelor de intersecție a curbelor:

4 - х 2 = х 2 - 2х

x = 2; y = 0 sau x = -1; y = 3

Astfel, cifra, a cărei zonă trebuie să o găsiți, poate fi reprezentată în Figura 4.10.

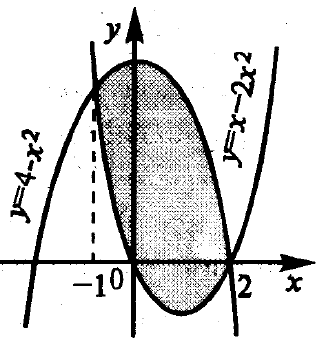
Figura 4.10 - Figura delimitată de liniile y = 4 - x 2 și y = x 2 - 2x

Pe intervalul [-1, 2] 4 - x 2 ≥ x 2 - 2x.

Folosim formula

, setarea f1 (x) = 4 - - x 2; f2 (x) = x2 - 2 x, a = -1, b = 2.

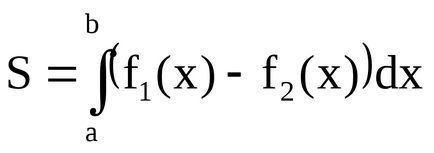
Exemplul 3. Găsiți aria figurinei delimitată de liniile y = 1 / x; y = x 2 și y = 4 în trimestrul de coordonate nonnegative.

Graficul grafic al funcției y = 1 / x este o hiperbolă, sub pozitiv x este convex în jos; axele de coordonate sunt asimptote. Graficul grafic al funcției y = x 2 în trimestrul de coordonate nonnegative este ramura parabolei cu punctul minim la origine. Aceste grafice se intersectează la 1 / x = x 2; x 3 = 1; x = 1; y = 1.

Drept y = 4, un grafic al funcției y = 1 / x traversează x = 1/4, un grafic al unei funcții y = x 2 x = 2 (sau -2).

Astfel, figura, a cărei suprafață trebuie să fie găsită, poate fi reprezentată în Figura 4.11.

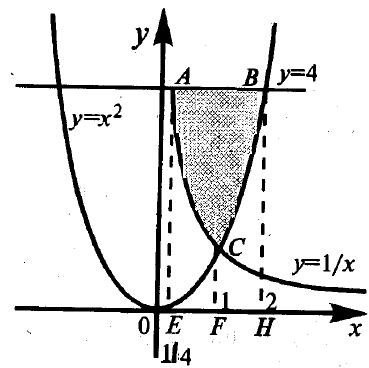
Figura 4.11 - Figura delimitată de liniile y = 1 / x; y = x 2 și y = 4 în trimestrul de coordonate nonnegative

Zona dorită a figurii ABC este egală cu diferența dintre suprafața dreptunghiului ABNE, care este 4 * (2 - ¼) = 7, și suma suprafețelor celor două trapezoidale curbilare ACFE și SWNF. Calculăm suprafața ACFE:

Să calculam suprafața SWNF:

Astfel, suprafața necesară este de 7 - (LN4 + 7/3) = 14/3 -ln43,28 (2 buc.).

Pagina anterioară

Pagina următoare