În această lecție vom cunoaște conceptul de arctangent. La început, luăm în considerare graficul funcției y = tan t la cea mai mică perioadă pozitivă, amintim proprietățile ei și formulăm problema directă și inversă pentru funcția noastră. Să definim arctangentul drept soluția problemei inverse. Apoi, luați în considerare găsirea tangentei arcului pe un cerc numeric folosind linia tangentă. Să arătăm proprietatea importantă a arctangentului: arctangentul de la minus a este egal cu minus arctangentul a. La sfârșitul lecției, rezolvăm câteva probleme de tip computațional și comparativ, ilustrând soluția pe grafic și pe cerc.
Subiect: Ecuații trigonometrice
Lecția: Arctangent și soluția ecuației tgx = a
1. Graficul grafic al funcției y = tgt, conceptul de tangentă a arcului
Introducerea conceptului de arctangent. ia în considerare funcția
Vom construi programul său detaliat.
Pe axa absciselor vom compila punctele multiple, iar pe axa de ordonare vom compila valorile corespunzătoare funcției cunoscute din tabele (figura 1).
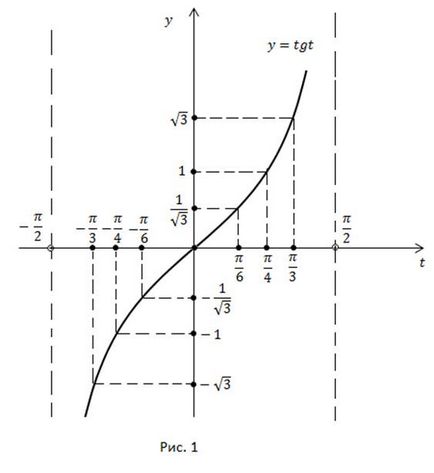
Diferența a fost aleasă, deoarece pe ea funcția ia toate valorile sale și crește monotonic.
Ne amintim problema directă și inversă pentru orice funcție.
Problema directă: prin valoarea dată a argumentului, găsiți valoarea corespunzătoare a funcției. De exemplu, dacă argumentul este egal, atunci valoarea funcției este 1.
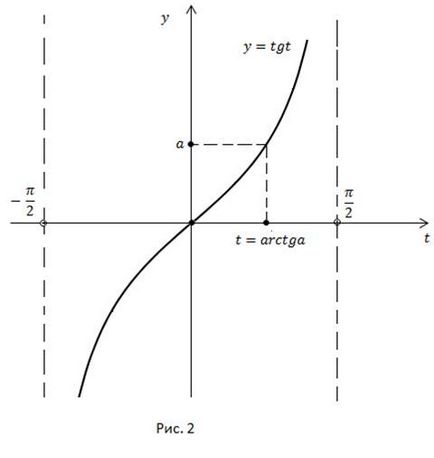
Problemă inversă: setați valoarea funcției, găsiți valoarea corespunzătoare a argumentului la interval. De exemplu, dacă
Fiecare valoare a unei funcții pe un interval este atinsă numai pentru o valoare a argumentului și se numește arctangent.
2. Definiția arctangentului și a interpretării grafice
Arctangentul este un număr al cărui tangent este egal cu
Valorile tangentei arcului sunt determinate din grafic (figura 1).
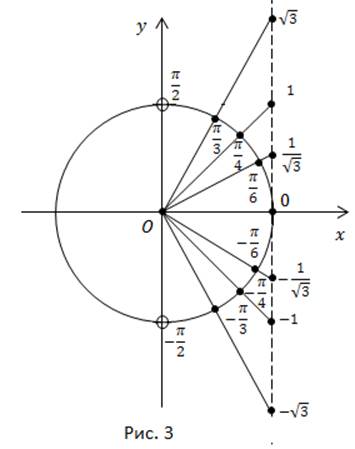
Arătăm cum să determinăm valorile tangentelor arcului pe un cerc trigonometric folosind linia tangentă.
Notați pe un cerc numeric punctele Conectăm fiecare dintre ele cu originea și tragem razele la intersecția cu linia tangentă. Obținem valorile tangentelor pentru aceste unghiuri (figura 3).
3. Proprietățile tangentei arcului
Observăm proprietatea importantă a arctangentului:
Il ilustram pe cercul unic (figura 4).
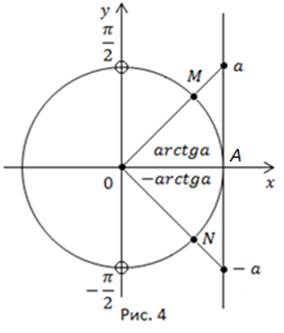
Dacă corespunde unui arc
4. Rezolvarea problemelor
Sarcina 1. Calculați:
Valorile arctangenților pot fi determinate din grafic (figura 1) sau din proprietate.
Sarcina 2. Aranjați în ordine crescătoare numărul:
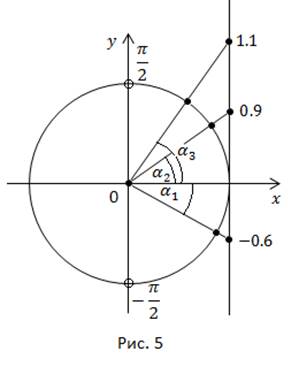
În acest interval, funcția crește în mod monoton
Problema 3. Calculați
Se ilustrează soluția pe un triunghi dreptunghiular (figura 6).
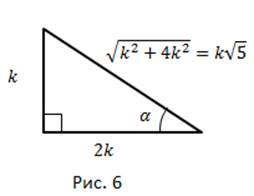
Unghiul este dat, adică picioarele sunt egale cu Hypotenuse de teorema lui Pitagora,
Problema 4. Calculați
Se ilustrează soluția într-un triunghi dreptunghiular (figura 7).
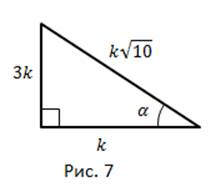
Problema 5. Calculați
5. Concluzie, concluzie
Ne-am familiarizat cu conceptul de arctangent și am rezolvat problemele tipice. În următoarea lecție rezolvăm ecuația cu ajutorul unei tangente cu arc.
21,31, 21,35, 21,48 (a, d).
2. Problemele portalului de Internet. ru.
3. Portalul educațional pentru pregătirea examenelor.
Se încarcă.
Se încarcă.
Lucrări populare
- Peisaje în versurile lui Alexander Puskin
- O analiză a poeziei de către A. Blok "Pe câmpul Kulikovo"
- Tată și fiu în povestea lui D. Aldridge "The Last Inch"
- Viața și munca Goethe V. Și
- Deciziile instanței de arbitraj. sarcini
- Proiectarea unei întreprinderi de catering public Proiectarea unui snack bar. partea 2
- A. S. Pushkin și S.A. Yesenin despre natura rusă
-
Statistici privind proiectele
Articole similare