CONDIȚII INIȚIALE NEREGULE ȘI NON-ELEMENTARE
Tensiunea și încărcarea elementului capacitiv imediat după comutarea uc (0+) păstrează acele valori pe care le-a avut înainte de a comuta uc (0-) și apoi se schimbă de la aceste valori.
A DOUA LEGISLAȚIE DE COMUTARE
PRIMUL LEGUM DE COMUTARE
Un proces de tranziție este procesul de tranziție de la o stare de echilibru a unui circuit electric la alt starea de echilibru.
Prelegerea №3 PROCESE TRANZITORII
În tranzistoare apar circuite electrice care conțin elemente reactive.
Fluxul curent și magnetic pe elementul inductiv imediat după comutare iL (0+) ...
stochează valorile pe care le-a avut înainte de a comuta iL (0-) și apoi se schimbă de la aceste valori.
Timpul t (0-) reprezintă timpul imediat înainte de comutare.
t (0) este timpul de comutare.
t (0+) este timpul imediat după comutare.
Această lege arată imposibilitatea unui salt curent prin inductanță.
Această lege dovedește imposibilitatea unui salt de tensiune pe capacitate.
Valorile inițiale pre-comutație
Valorile curenților, tensiunilor, direct la
comutare (la t = 0-).
După comutare valorile inițiale-valori ale curenților și tensiunilor imediat după comutare (la t = 0 +).
CONDIȚII INIȚIONALE INDEPENDENTE ȘI DEPENDENTE.
Valorile curenților prin inductanța iL (0-) și tensiunile la capacitățile uc (0). cunoscute din regimul de pre-comutație, se numesc condiții inițiale independente
Valorile curenților și tensiunilor rămase la t = 0 + în schema post-comutație, determinată din valorile inițiale independente de la legile lui Kirchhoff, sunt numite valori inițiale dependente.
Dacă, la începutul procesului tranzitoriu, chiar înainte de comutare, toți curenții și tensiunile pe elementele pasive ale circuitului sunt zero, atunci circuitul are zero-
Dacă, la începutul procesului tranzitoriu, curenții și tensiunile din circuit nu sunt egale cu zero, atunci circuitul are condiții inițiale nonzero.
Următoarele metode de calcul sunt utilizate pe scară largă:
1. Metoda clasică
2. Metoda operatorului
3. Metoda de calcul folosind integralele Duhamel.
CALCULUL CONȚINE URMĂTOARELE OPERAȚII DE BAZĂ
a) alegerea direcțiilor pozitive ale curenților în ramurile lanțului;
b) determinarea valorilor curenților și tensiunilor
imediat înainte de comutare;
c) formularea ecuației caracteristice
și definirea rădăcinilor sale;
d) obținerea de expresii pentru curenții și
subliniază funcțiile timpului.
METODA CLASICĂ DE CALCUL
Procesul tranzitoriu în orice lanț liniar este împărțit condiționat în mod liber și forțat
curent sau tensiune,
tensiune în funcție de timp.
Ecuația caracteristică a circuitului este formulată ca o expresie pentru rezistența de intrare a circuitului la curentul alternativ, unde j # 969; se înlocuiește cu p, unde p este rădăcina ecuației caracteristice
Impedanța de intrare este:
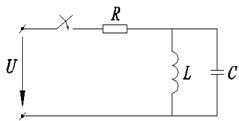
Înlocuiți j # 969; → p. Ecuația caracteristică poate fi scrisă în următoarea formă
Pentru a determina rădăcinile ecuației caracteristice, ea este egală cu zero și rezolvată în raport cu p, Z (p) = 0
deoarece la o ecuație dată de ordinul doi vor exista și două rădăcini:
componenta liberă a curentului sau a tensiunii tranzitorii este scrisă ca o funcție exponențială
iвв = Ae pt. unde A este constanta de integrare
se determină din condițiile inițiale pentru t = 0
p este rădăcina ecuației caracteristice.
Componenta forțată a curentului sau a tensiunii este determinată pentru modul post-comutație la starea de echilibru. Această valoare a curentului sau a tensiunii după atenuarea tuturor tranzitorilor se determină prin orice metodă disponibilă.
Orice proces tranzitoriu într-un circuit electric liniar durează teoretic pe o perioadă nedeterminată, deoarece Ae pt nu va fi niciodată zero. Dar după o anumită perioadă de timp, componenta liberă a procesului tranzitoriu poate fi neglijată.
Acest interval este limitat la 5 # 964; unde # 964; Este timpul constant, în care valoarea inițială a funcției scade cu "e" ori.
Este reciprocitatea rădăcinii ecuației caracteristice.
Avantajul metodei clasice este claritatea sa: atunci când se calculează circuitul, natura schimbării tuturor curenților și tensiunilor este vizibilă.
Dezavantajul metodei este nevoia de a rezolva atât sistemul de ecuații diferențiale pentru determinarea tuturor curenților și tensiunilor circuitului, cât și sistemul de ecuații algebrice pentru determinarea constantelor de integrare. Acest dezavantaj este lipsit de metoda de calcul a operatorului.
METODA OPERAȚIONALĂ DE CALCULARE
Metoda de operare pentru calcularea proceselor tranzitorii se bazează pe înlocuirea funcțiilor de timp (originalul) f (t) printr-o funcție a unei variabile complexe p, adică imaginea lui F (p) prin transformarea Laplace.
Trecerea de la original la imagine utilizând transformarea directă Laplace.
Metoda de operator permite să se reducă funcționarea diferențierii la multiplicare și funcționarea integrării la împărțire. Aceasta facilitează integrarea ecuațiilor diferențiale.
Imagini ale unora dintre cele mai simple funcții.