Fresnel a propus o metodă originală de împărțire a suprafeței undei S în zone, ceea ce a făcut posibilă o simplificare foarte mare a soluției de probleme (metoda zonei Fresnel).
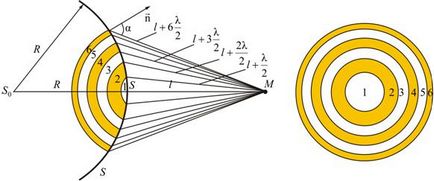
Limita primei zone (centrale) este punctul de suprafață S. situat la o distanță de punctul M (Figura 9.2). Punctele sferei S. sunt la distanțe. . și așa mai departe. din punctul M. forma 2, 3, etc. Zonele Fresnel.
Oscilațiile excitate la punctul M între două zone învecinate sunt opuse în fază, deoarece diferența de cale de la aceste zone la punctul M.
Prin urmare, atunci când aceste oscilații sunt adăugate, ele trebuie să se slăbească reciproc:
,
unde A este amplitudinea oscilației rezultate, este amplitudinea oscilațiilor excitate de zona i-a Fresnel.
Valoarea depinde de zona zonei și de unghiul dintre suprafața normală și suprafața dreaptă direcționată către punctul M.
Zona unei zone
.
Prin urmare, este clar că zona zonei Fresnel nu depinde de numărul zonei i. Aceasta înseamnă că pentru zonele care nu sunt prea mari, zonele din zonele învecinate sunt aceleași.
În același timp, pe măsură ce numărul zonei crește, unghiul crește și, în consecință, intensitatea radiației zonei scade în direcția punctului M. amplitudinea scade. De asemenea, scade datorită creșterii distanței până la punctul M:
.
Numărul total al zonelor Fresnel care se potrivesc unei părți a sferei orientate spre punctul M. este foarte mare: la. . numărul de zone. și raza primei zone.
Prin urmare, rezultă că unghiurile dintre zona normală și zona și direcția spre punctul M în apropierea zonelor vecine sunt aproximativ egale, adică că amplitudinile valurilor care ajung la punctul M din zonele învecinate sunt aproximativ egale.
Un val de lumină se propagă rectiliniu. Fazele de oscilație excitate de zonele învecinate diferă de π. Prin urmare, ca o aproximație admisibilă, putem presupune că amplitudinea oscilației din o anumită zonă m este egală cu media aritmetică a amplitudinilor zonelor adiacente, adică
.
Apoi, expresia (9.2.1) poate fi scrisă în formular
.