Funcția Euler φ (a) este definită pentru toate numerele naturale a și reprezintă numărul de numere naturale care sunt relativ prime la a. și nu depășește a. Se presupune că φ (1) = 1. Această funcție este calculată din formula
unde
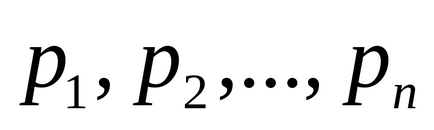
Numărul de numere care compun sistemul redus de reziduuri este φ (m).
Proprietatea generală a unui sistem complet și redus de reziduuri
În cazul în care numerele
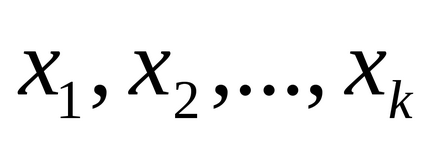
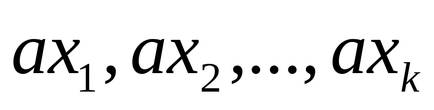
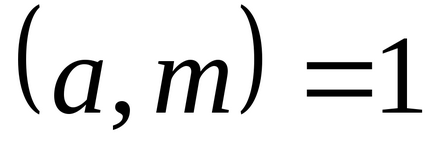
Arată că numerele 25, -20,16,46, -21,18,37, -17 constituie un sistem complet de reziduuri modulo 8.
Formăm întregul sistem de numere cu cel puțin ne-negativ
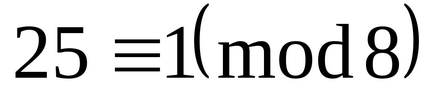
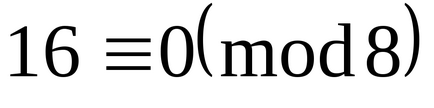
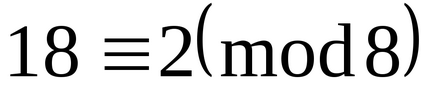
Deci, aceste numere 0,1,2,3,4,5,6,7 formează un sistem complet de reziduuri modulo 8.
Teoremele Euler și Fermat
Lăsați x să treacă prin sistemul redus de reziduuri
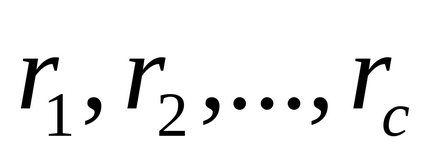
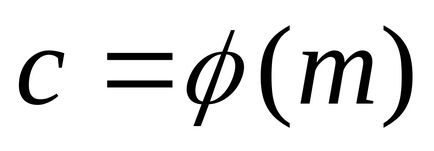
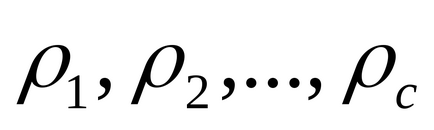
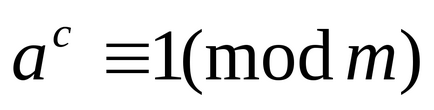
Pentru simplu p și a. nu divizibilă de p. noi avem
Această teoremă este un caz special al teoremei Euler, pentru m = p. Din (2) se poate obține cu ușurință o comparație foarte importantă
,
care este valabil pentru toate numerele întregi a. deoarece este valabil și pentru un multiplu de p.
Verificați teorema lui Euler pentru a = 5 și.
,
.
Găsiți restul diviziei
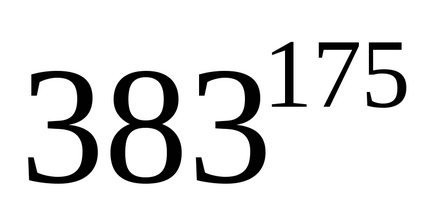
Pentru că, atunci. deoarece
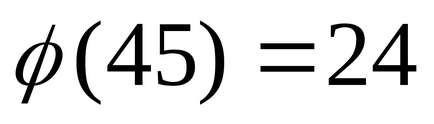
.
Răspuns: restul necesar este de 32.
Comparațiile dintre gradul I (rezolvarea problemelor)
Rezolvați metoda de comparare a lui Euler. Verificați corectitudinea răspunsului înlocuind.
(3,5) = 1, atunci această comparație are o soluție unică (în sensul clasei de numere x mod m). Prin formula Euler,
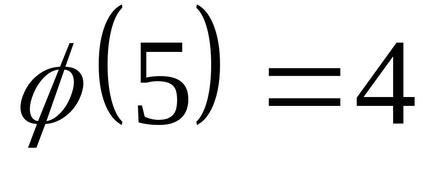
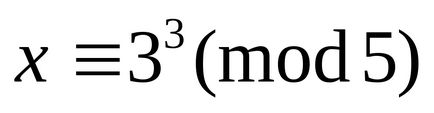
Rezolvați metoda de comparare a lui Euler.
(5.10) = 5, dar 7 nu este divizibil cu 5, deci această comparație nu are soluții.
Rezolvați metoda de comparare a lui Euler.
Deoarece (25.17) = 1, această comparație are o soluție. Această comparație este echivalentă cu comparația. Prin formula lui Euler avem.
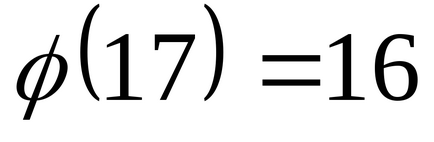
.
Rezolvați o modalitate de a compara
(12,15) = 3. Prin urmare, această comparație are 3 soluții (în sensul claselor). Luați în considerare o comparație
care derivă din valoarea dată după o reducere de 3.
Prin formula lui Euler avem,.
Am găsit o soluție a congruenței (2). Soluția de comparație (1) este dată de formula, k = 0,1,2.
; ; .
Pentru a atribui dreptului la numărul 523 astfel de trei numere, astfel încât numărul rezultat din șase cifre să fie împărțit la 7.8.9.
Lăsați numărul x să fie atribuit. apoi, de unde. Valoarea x va fi un număr de trei cifre pentru t = 0 și t = 1. Avem
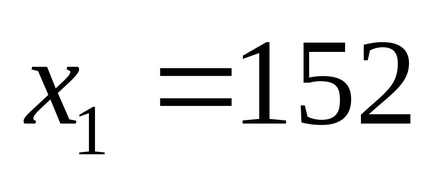
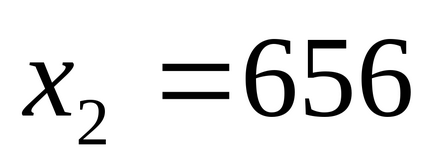
523,152 împărțit la 7,8,9;
523656 este împărțit în 7,8,9.