
Acasă | Despre noi | feedback-ul
Difracția undelor - fenomenul de înfășurare a undelor de obstacole și pătrunderea lor în regiunea umbrei geometrice. Fenomenul de difracție poate fi explicat calitativ prin aplicarea principiului Huygens la propagarea undelor într-un mediu în prezența unor obstacole.
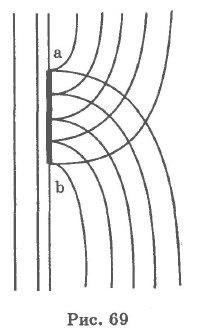
Luați în considerare o barieră fixă ab (Figura 69). Figura arată suprafețele undei construite de principiul Huygens din spatele obstacolului. Se poate vedea că valurile acțiunii
îndoiți în zona umbrei. Dar principiul Huygens nu spune nimic despre amplitudinea oscilațiilor într-un val în spatele unei barieră. Acesta poate fi găsit prin luarea în considerare a interferenței valurilor care intră în regiunea umbrei geometrice. Distribuția amplitudinilor de oscilație în spatele obstacolului se numește modelul de difracție. Forma completă a modelului de difracție din spatele barierei depinde de relația dintre lungimea de undă A, dimensiunea barierului d și distanța L de la obstacol până la punctul de observare. Dacă lungimea de undă A este mai mare decât dimensiunea barierului d, atunci valul abia o observa. Dacă lungimea de undă L este de același ordin de mărime cu dimensiunea barierului d, atunci difracția se manifestă chiar și la o distanță foarte mică L, iar undele din spatele barierului sunt doar puțin mai slabe decât în câmpul undei libere de pe ambele părți. Dacă, în final, lungimile de undă sunt mult mai mici decât dimensiunile obstacolului, atunci modelul de difracție poate fi observat numai la o distanță mare de barieră, a cărui mărime depinde de A și d.
Principiul Huygens-Fresnel este o extensie a principiului introdus de Christian Huygens în 1678: fiecare punct al frontului (suprafața atinsă de val) este o sursă secundară (adică nouă) a undelor sferice. Plicul fronturilor valurilor tuturor surselor secundare devine frontul undei în următoarea secvență de timp.
Principiul lui Huygens explică propagarea valurilor, în concordanță cu legile opticii geometrice, dar nu poate explica fenomenele de difracție. Augustin Jean Fresnel a completat principiul Huygens în 1815, introducând concepte de coerență și interferență a undelor elementare, care au permis să ia în considerare fenomenele de difracție bazate pe principiul Huygens-Fresnel.
Principiul Huygens-Fresnel este formulat după cum urmează:
Fiecare element al frontului undei poate fi privit ca centrul unei perturbații secundare care generează valuri sferice secundare, iar câmpul luminos rezultat în fiecare punct al spațiului va fi determinat de interferența acestor valuri.
Gustav Kirchhoff a dat principiului Huygens o formă matematică riguroasă, arătând că poate fi considerată o formă aproximativă a unei teoreme numită teorema integrală a lui Kirchhoff.
Fața unui val de sursă punctuală într-un spațiu izotropic omogen este o sferă. Amplitudinea perturbației la toate punctele frontului sferic al unei valuri care se propagă dintr-o sursă punctuală este aceeași.
O generalizare și dezvoltare ulterioară a principiului Huygens este formularea în termeni de integrali ai căilor, care sta la baza mecanicii cuantice moderne.
Metoda zonei Fresnel Frenel a propus o metodă de divizare a frontului undei în zone inelare, care mai târziu a fost denumită metoda zonei Fresnel.
Lăsați o undă sferică monocromatică să se propagă din sursa de lumină S și P punctul de observație. O suprafață a undelor sferice trece prin punctul O. Este simetric în privința liniei SP.
Împărțim această suprafață în zonele inelare I, II, III etc. astfel încât distanțele de la marginile zonei la punctul P diferă cu l / 2 - jumătate din lungimea undei luminoase. Această partiție a fost propusă de O. Fresnel, iar zonele sunt numite zonele Fresnel.
Luăm un punct arbitrar 1 în prima zonă Fresnel. În Zona II există, în virtutea regulii de construcție a zonelor, un punct corespunzător că diferența de traiectorie dintre razele care merg la punctul P din punctele 1 și 2 va fi egală cu l / 2. Ca urmare, oscilațiile de la punctele 1 și 2 se anulează reciproc la punctul P.
Din considerente geometrice rezultă că, pentru un număr foarte mare de zone, zonele lor sunt aproximativ aceleași. Prin urmare, la fiecare punct al primei zone există un punct corespunzător în a doua zonă, oscilațiile cărora se anulează reciproc. Amplitudinea oscilației rezultate, care ajunge la punctul P din zona cu numărul m, scade cu creșterea m, adică