Mai departe, pe harta rezultată găsim toate blocurile posibile de unități de formă 2 k × 2 l; k, l ∈ N. Având în vedere faptul că harta este bucle. Blocurile se pot suprapune, dar nu trebuie să se includă reciproc. Apoi, pentru fiecare bloc este scos un vector, în care, dacă variabila din acest bloc a modificat valoarea, semnul "-", dacă nu este, valoarea sa în cadrul blocului. Pentru pozițiile vectorului i. în care este semnul σ ∈? în CE se adaugă xi σ. Disjuncția tuturor CE primite este un DNF scurtat.
[edit] Exemplu
Găsim DNF abreviat pentru funcția f = (1010 0110 0111 1101) folosind metoda Carnot.
Soluția
Construirea unei hărți:

Pe baza hărții obținem următoarele blocuri:
[edit] Construirea unui DNF scurtat pentru un DNF perfect folosind algoritmul Quine
Algoritmul lui Quine pentru construirea unui DNF redus cu un DNF perfect: 0) i: = 1 1) Cu toate acestea, este posibil să se aplice lipirea incompletă la termenii de rang n-i + 1:
2) în timp ce absorbția 3) i ++ este posibilă; dacă (i<=n) goto 1
[edit] Construirea DNF Quine
DNF, care este obținut prin aruncarea tuturor implicanților simpli care corespund fețelor maxime acoperite de nucleu, se numește DNF Quine.
Algoritm pentru construirea DNF Quine:
1. obțineți un DNF scurtat;
2. găsiți fețele de sunet;
3. Îndepărtați implicații acoperiți de nucleu.
DNP obținut este DNF Quine.
[edit] Construcția lui DNF σT (suma de la sfârșitul anului)
[edit] Construirea tuturor DNF pasionat
Să căutăm toate soluțiile pentru FAL f. Se scrie tabelul M (tabel Quine), în care coloanele din Nf (seturile pe care funcția ia valoarea 1) corespund coloanelor, fețele maxime corespund rândurilor. Celula este 1 dacă fața corespunzătoare liniei conține setul corespunzător coloanei.
Apoi scrieți funcțiile de acoperire CNF după cum urmează:
Să presupunem că fiecare linie corespunde unei anumite schimbări a lui yi.
Pentru fiecare coloană, variabilele corespunzătoare rândurilor din această coloană sunt 1, o scriem prin logică sau. Funcția de acoperire este egală cu produsul acestor sume pentru fiecare coloană.
[edit] Exemplu
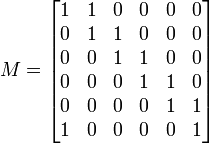
Extinzând parantezele și oferind altele similare, primim:
Apoi, definiți punctele de bază, adică acele ai. care au o singură unitate în coloană. Acestea sunt α1. α3. α5. α7. α9. α10. În consecință, muchiile sonore sunt acele margini care corespund conjunctions care picuri aparțin sunetului (uita-te la linia în care cel puțin una dintre coloanele selectate αi este o unitate), adică K1. K2. K4. K5. K7. Disjuncția acestor conjuncții este intersecția unor termene moarte.
Pentru a găsi toate impas DNF construi CNF, care elementarnyo disjuncție va consta din PD, care corespunde conjuncțiilor, care includ punctul de αi considerat (adică, toate disjuncții la fel de mult ca și există puncte în care funcția este setată la unul, cu primul disjuncția va conține PD cele care corespund cE, care face parte din catenele a1 (în acest exemplu, K1), al doilea - cele care corespund cE, care face parte α2 (K1 K2 K3 ..), și așa mai departe):
După combinarea prezentarea unor informații similare și de a obține DNP constând din CE, care se va întâlni o fundătură DNP, cu PD CE CE se va potrivi în DNP ciot:
Materiale pentru examen