Să rezolvăm câteva probleme legate de determinarea intensității câmpului la diferite distanțe față de obiect, care este sursa câmpului. Aici trebuie să ne amintim regulile pentru preluarea derivatului unei funcții complexe și, de asemenea, limita unei funcții.
Problema 1. La o intensitate a câmpului electric V / m, aerul încetează să mai fie un izolator de încredere și apare o descărcare de scânteie. Care ar trebui să fie raza mingii metalice, astfel încât să poată avea o încărcătură de 1 Cl?
Forța câmpului unei sfere încărcate este exprimată prin formula
Prin urmare, găsim raza:
Problema 2. Există patru încărcări identice în vârfurile pătratului cu partea laterală. Determinați forța maximă a câmpului pe axa care trece prin mijlocul pătratului perpendicular pe planul său. La ce distanță de pătrat este tensiunea maximă?
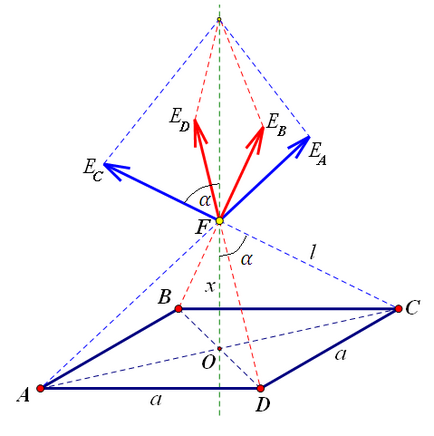
Fiecare dintre încărcări va contribui la puterea totală a câmpului într-un anumit punct. Vectori de tensiune din perechea de taxe în colțuri opuse, compensează parțial reciproc: componentele lor orizontale (proiecție pe un plan patrat) suma va da un zero. Prin urmare, vor fi adăugate componentele verticale - proiecția forțelor pe axa verticală. Proiecția forței câmpului pe axa verticală dintr-o singură încărcare este:
Din patru taxe:
Distanța până la încărcare. definiți-o. Dacă partea este pătrată. atunci diagonala este egală cu. și jumătate din diagonală. Lăsați distanța de la planul pătratului până la punct. . atunci
În această formulă, variabila este distanța. Pentru a găsi maximul unei funcții. vom lua derivatul:
Ecuați derivatul la zero pentru a găsi extrema:
Am determinat distanța la care intensitatea este la un maxim - poate fi văzută în faptul că acesta este punctul de mare, pentru a determina semnul derivat din stânga și dreapta punctului. Acum putem înlocui această distanță în formula rezistenței câmpului și putem determina intensitatea maximă:
Răspuns: Tensiunea maximă este atinsă la o distanță față de planul pătratului.
Problemă 3. Un inel de sârmă subțire cu o rază are o încărcătură. Găsiți forța câmpului pe axa inelului la o distanță de centrul acestuia. Construiți un grafic de dependență.
Sarcina este similară celei precedente. Numai acum încărcările elementare sunt distribuite în jurul inelului, iar fiecare încărcătură creează un vector de tensiune. Astfel, obținem o suprafață sub forma unui con constituit din vectorii forțelor individuale ale încărcăturilor elementare.
Dacă stați în centrul inelului, atunci vectorii se compensează complet și tensiunea totală va fi zero. Cu toate acestea, odată ce trecem un pic la dreapta sau la stânga acestui punct, tensiunea nu va fi zero, deoarece vectorii din componenta longitudinală va fi, și că este suma tuturor acestor componente și oferă intensitatea câmpului în orice punct de pe axa inelului, departe de lui distanta. Încărcarea elementară poate fi găsită ca. Tensiunea creată de el,
În cazul în care. dar cosinusul unghiului
Rezistența câmpului la toate încărcăturile:
Pentru a găsi maximul unei funcții. vom lua derivatul:
Ecuați derivatul la zero pentru a găsi extrema:
Să determinăm intensitatea câmpului maxim în acest moment, înlocuind această distanță în expresia pentru tensiune:
Am aflat că în centrul inelului intensitatea câmpului este zero și crește cu distanța. până când ajunge la un maxim la distanță. Acum, să vedem ce va fi egal cu tensiunea la o distanță infinit de mare: să tindem spre infinit.
Deoarece această funcție atât numărătorul și numitorul și avem tipul de incertitudine infinit la infinit, atunci definim limita de regula L'Hospital lui:
Deci, puteți construi un grafic:
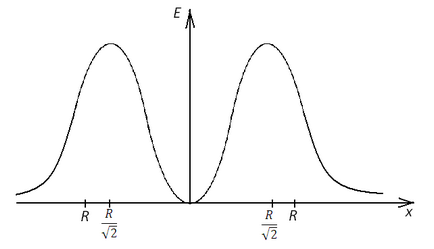
Sarcina 3, graficul