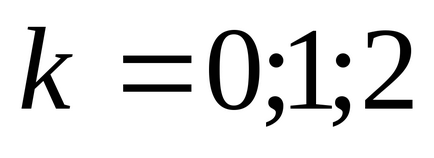Acțiuni pe numere complexe în formă algebrică și trigonometrică.
Conceptul unui număr complex și interpretarea sa geometrică.
Acțiuni pe numere complexe în formă algebrică.
Forma trigonometrică a unui număr complex.
Acțiuni pe numere complexe în formă trigonometrică.
1. Conceptul unui număr complex și interpretarea sa geometrică.
Definiție 1. Numere complexe sunt numerele formularului
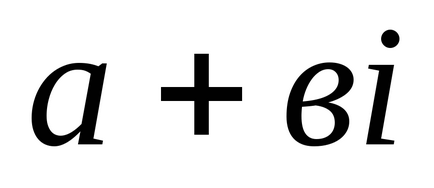


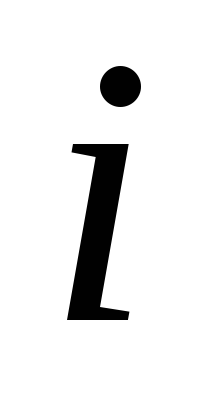
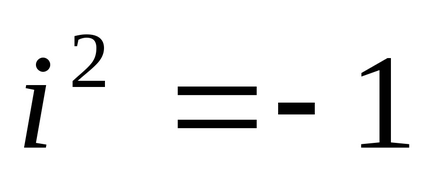
1). Două numere complexe
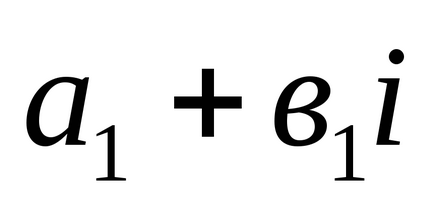
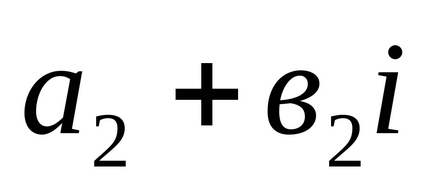
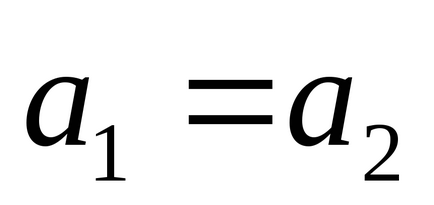
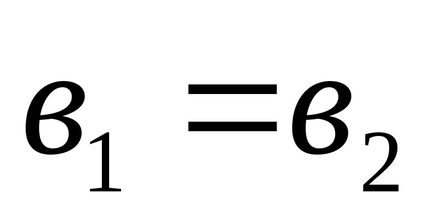
2). Suma a două numere complexe
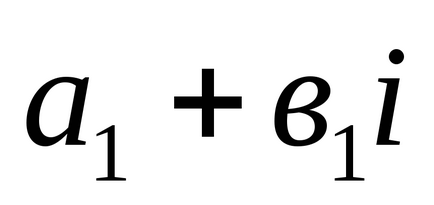
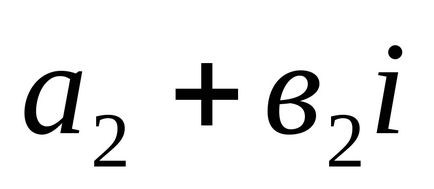
3). Produsul a două numere complexe
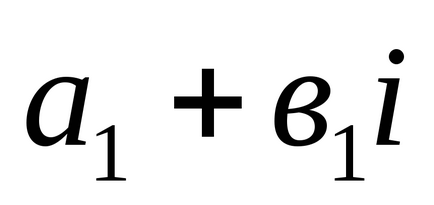
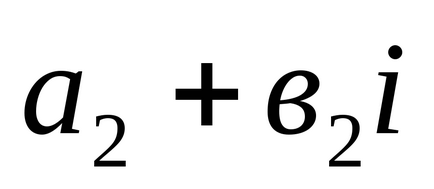
Notarea unui număr complex în formă
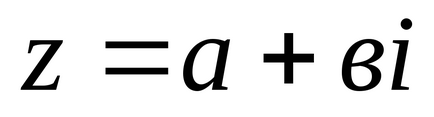


Orice număr real este conținut într-un set de numere complexe. Prin urmare, poate fi scrisă ca:
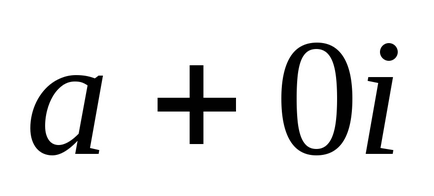
Definiția 2: Numărul complex
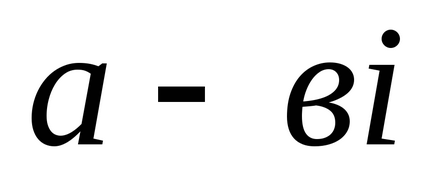
cu un număr
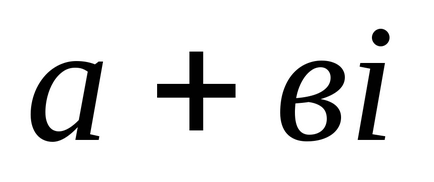
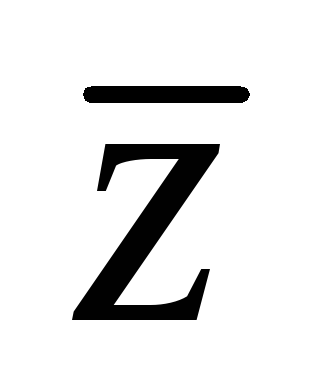
Definiția 3: modulul complex de numere
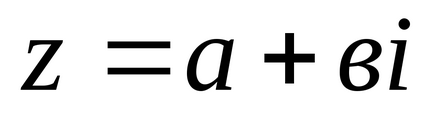
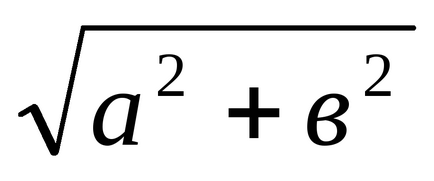
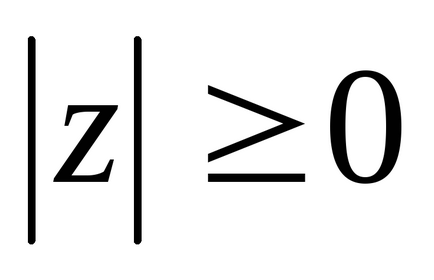
Un număr complex poate fi reprezentat în două moduri:
1. Punctul planului cu coordonatele (a; b).
În acest caz, numerele reale sunt reprezentate de punctele axei abscise, care se numește axa reală. și numere pur imaginare, punctele axei ordinii, care se numește axa imaginară.
2. Sub forma unui vector cu originea la origine (
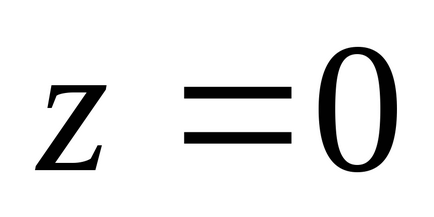
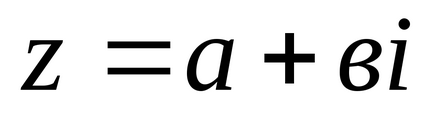
La fiecare punct al planului cu coordonatele (a; b) corespunde un singur vector cu originea în punctul O (0; 0) și capătul de la punctul M (a; b), astfel încât numărul complex
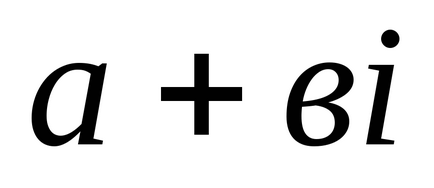
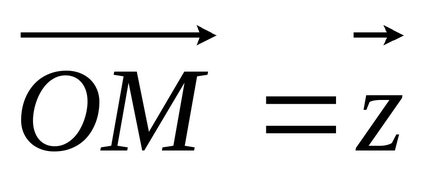
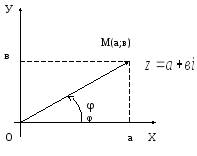
Definiția 4: Unghiul φ între axa reală OX și vector
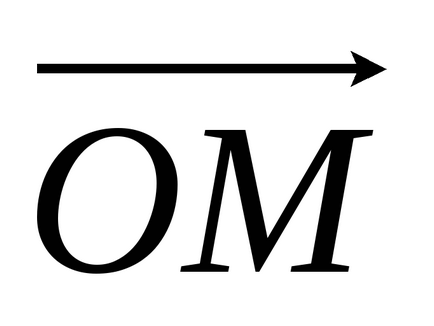
Orice număr complex are un set infinit de argumente care diferă unul de celălalt printr-un număr multiplu

Din definiția funcțiilor trigonometrice rezultă:
Pentru a descrie interpretarea geometrică a unui număr complex, pentru a găsi modulul unui număr complex și valoarea principală a argumentului.
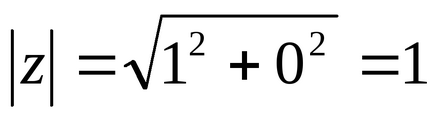
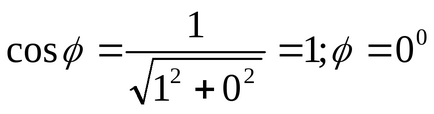
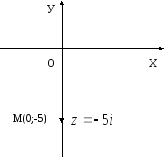
;
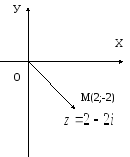
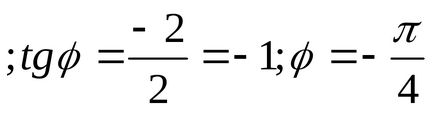
2. Acțiuni asupra numerelor complexe în formă algebrică.
Adunarea și multiplicarea numerelor complexe pe care le-am introdus în definiția unui număr complex. Introducem regulile pentru scăderea și divizarea numerelor complexe:
.
Dar este foarte convenabil să se efectueze acțiuni pe numere complexe cu ajutorul regulilor acțiunilor corespunzătoare asupra polinomilor și a conceptului de unitate imaginară.
k). .
3. Forma trigonometrică a unui număr complex.
Reprezentăm numărul complex
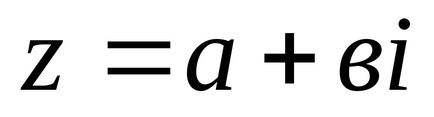
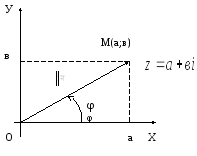
Indicăm modulul unui număr complex.
Argumentul unui număr complex este unghiul φ, care este calculat folosind formulele:
Înlocuim formulele rezultate în
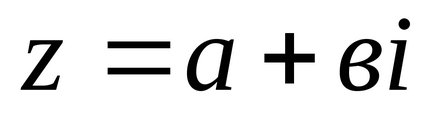
- forma trigonometrică a unui număr complex.
Algoritmul pentru trecerea de la o formă algebrică a unui număr complex la unul trigonometric:
Desenați un număr geometric
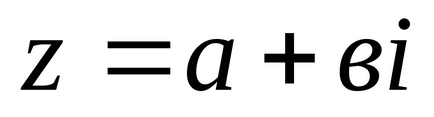
Scrieți ecuațiile:
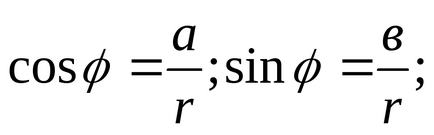
Scrieți z în forma trigonometrică.
Exemple: a) Transferați numere dintr-o formă algebrică într-o formă trigonometrică.
2. Reprezentăm geometric:
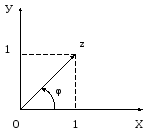
Prin urmare, φ aparține primului trimestru.
2. Reprezentăm geometric:
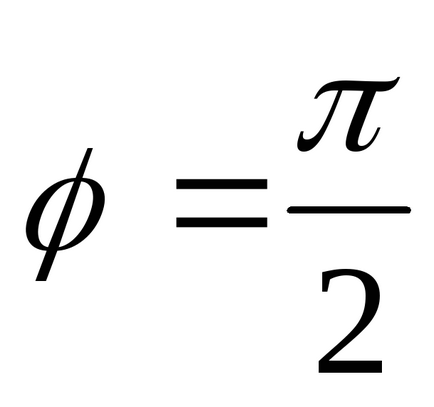
Deci, 3 puncte pot fi omise.
2. Reprezentăm geometric:
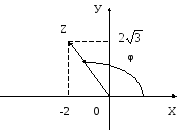
φ aparține trimestrului al doilea.
b). traduce din formă trigonometrică la algebrică:
.
.
4. Actiuni asupra numerelor complexe in forma trigonometrica.
Fie ca două numere să fie date în forma trigonometrică: și.
1). Când se înmulțesc două numere complexe date în formă trigonometrică, modulele lor se înmulțesc și se adaugă argumentele:
.
2). Atunci când împărțiți două numere complexe date în formă trigonometrică, modulele lor sunt împărțite și argumentele sunt scăzute:
.
3). Când numărul complex este ridicat la puterea n-a, se folosește formula:
, care se numește formula Moivre.
4). Pentru a extrage rădăcina n de la numărul complex, utilizați formula:
.