5.3. Metode recursive
Esența metodelor recursive este reducerea problemei la sine. Știți deja că, atât în Pascal, cât și în C, există posibilitatea definirii recursive a funcțiilor și procedurilor. Această caracteristică este o modalitate de a implementa în mod programatic algoritmi recursivi. Cu toate acestea, este adesea foarte dificil de a vedea modul recursiv de rezolvare a unei probleme (un algoritm recursiv).
Luați în considerare problema clasică cunoscută în literatură sub numele de "Turnul Hanoi" (Figura 50).
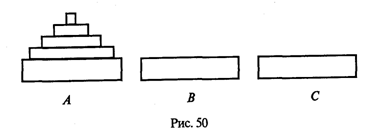
Pe site-ul (să o numim A) există o piramidă formată din discuri care scad de la bază la partea superioară a dimensiunii.
Această piramidă în aceeași formă trebuie să fie mutată pe site-ul B. Când efectuați această lucrare, trebuie respectate următoarele restricții:
• Puteți schimba doar un disc preluat de deasupra piramidelor;
• Puteți plasa discul fie la baza platformei, fie pe un disc mai mare;
• Ca site auxiliar, site-ul C poate fi utilizat.
Denumirea "Turnul Hanoi" este asociată cu o legendă potrivit căreia călugării unui templu din Hanoi au căutat, în vechime, să se mute în conformitate cu aceste reguli un turn format din 64 de discuri. Odată cu finalizarea lucrărilor lor, va veni sfârșitul lumii. Călugării încă lucrează și, sperăm, vor lucra mult timp!
Nu este dificil să rezolvi această problemă pentru două discuri. Denumind deplasările unui disc, de exemplu, dintr-un sit A la B ca: A → B, vom scrie un algoritm pentru acest caz
A → C; A → B; C → B.
Doar 3 rotiri! Pentru trei unități, algoritmul este mai lung:
A → B; A → C; B → C; A → B; C → A; C → B; A → B.
În acest caz, sunt deja necesare 7 mutări.
Calculați numărul de mișcări (N) pentru discurile k prin următoarea formulă de recurență:
N (1) = 1; N (k) = 2 x N (k - 1) + 1.
De exemplu, N (10) = 1023, N (20) = 104857. Dar câte mișcări trebuie făcute pentru călugării din Hanoi:
Încercați să citiți acest număr.
Acum vom compila un program conform căruia mașina va calcula algoritmul muncii călugărilor și îl va scoate pentru orice valoare de n (numărul de discuri). Să presupunem că există discuri n pe setul A. Algoritmul de rezolvare a problemei este următorul:
1. Dacă n = 0, atunci nu faceți nimic.
2. Dacă n> 0, mutați discul n-1 în C prin B;
mutați discul de la A la B (A → B)
mutați n - 1 disc de la C la B prin A.
Când realizăm pasul 2, vom avea în mod consecvent trei stări (Figura 51).
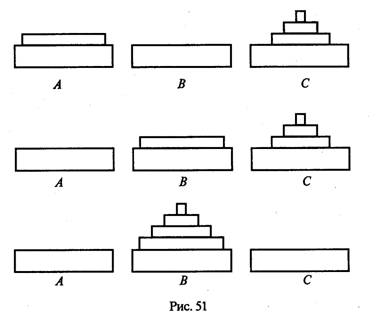
Descrierea algoritmului are un caracter clar recursiv