Luați în considerare efectul forței centrifuge pe un arbore cu un disc (arborele este poziționat vertical pentru a exclude deformarea sub acțiunea masei proprii a discului și efectul forței centrifuge este considerat în forma sa pură).
Centrul de greutate al arborelui staționar cu discul este situat la o distanță față de axa sa (Figura 5.5a). Forța centrifugă care apare atunci când rotorul se rotește cauzează o deformare la arbore, a cărei valoare depinde de forță. dimensiunile și materialul arborelui, precum și localizarea discului în raport cu suporturile. Forța centrifugă, crescând odată cu creșterea vitezei, este o forță periodică aplicată pe grinda elastică (arbore) și provocând oscilații armonice ale sistemului. Este echilibrat de forța elastică. care este proporțională cu deformarea.
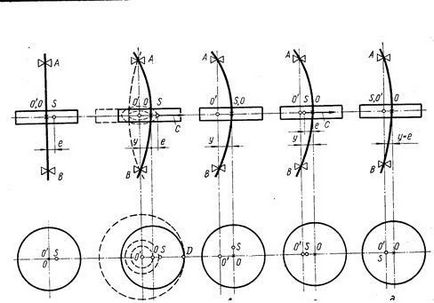
Poziția centrului de greutate al discului la viteze diferite
Rotirea arborelui se realizează în jurul axei verticale (figura 5.5b), unde sunt prezentate traiectoriile punctelor și în jurul centrului de rotație (punct).
Ecuația de echilibru a unui sistem elastic are forma
unde este masa discului, kg; - viteza unghiulară, rad / s; și. m.
unde este forța elastică egală cu forța care determină deformarea arborelui de 1 cm, dar opusă direcționării acestuia.
Înlocuindu-ne valorile lui u în (5.6), obținem
În consecință, deoarece viteza unghiulară (frecvența de rotație a oscilațiilor forțate ale rotorului) crește, devierea (amplitudinea oscilațiilor forțate ale arborelui) crește și la o anumită valoare valoarea.
Din teoria oscilațiilor sistemelor elastice se știe că la rezonanță (coincidența frecvențelor oscilațiilor eigen și oscilante ale sistemului elastic), amplitudinea oscilațiilor este teoretic egală cu infinitatea. adică, arborele trebuie să se rupă.
Rezultă din (5.9) că
Prin urmare, frecvența circulară rezonantă sau, așa cum se mai numește, viteza unghiulară critică a rotației
și viteza critică ()
Înlocuind valoarea de masă. avem
în cazul în care. kg; - gravitatea discului; ; m / s 2.
În realitate, oscilațiile de rezonanță apar la o frecvență critică de rotație, dar arborele nu se rupe imediat datorită acțiunii forțelor de rezistență. Acestea includ forțe interne de frecare ale materialului arborelui, frecare a suprafeței rotorului în jurul mediului și frecare în lagăre. Amplitudinea oscilațiilor la rezonanță crește mai puțin, cu atât este mai mare coeficientul de rezistență.
Funcționarea turbinei la o viteză critică de rotație este însoțită de o vibrație considerabilă și poate conduce la un accident dacă este folosit mult timp. Dacă viteza critică de rotație este rapidă, adică frecvența circulară a oscilațiilor forțate este crescută în comparație cu frecvența circulară a oscilațiilor naturale, atunci o scurtă durată a tranziției prin frecvența critică de rotație va determina dezvoltarea vibrațiilor. Cu o tranziție foarte rapidă, se poate realiza că oscilațiile rezonante nu cresc, iar arborele va funcționa fără oscilații notabile. Cu o tranziție relativ lentă a frecvenței critice de rotație, vor apărea oscilații de rezonanță, dar se vor deteriora cu distanța de la frecvența critică de rotație.
Substituim valorile de la (5.8) în (5.7), apoi
Această expresie este pozitivă și negativă pentru. Frecvența unghiulară de rotație este frecvența circulară a oscilațiilor forțate ale arborelui, iar a este frecvența circulară a oscilațiilor naturale.
Folosind concluziile teoriei oscilațiilor legate de schimbarea de fază între vibrațiile proprii (caracterizate prin deformare) și forța perturbativă (centrifugă) determinată de direcția excentricității. putem scrie ecuația de schimbare a fazei pentru oscilațiile arborelui, care denotă și.
Dependența de raportul dintre frecvențele construite din (5.13) pentru diferite valori ale coeficientului de amortizare. se numește răspunsul de fază (figura 5.6). Forțele oscilante întotdeauna sunt întârziate în fază de forța motrice, iar valoarea lagului se situează în intervalul de la 0 la. Odată cu creșterea măririi fazei, crește treptat. În intervalul, unghiul este pozitiv și mai mic de 90 0. În momentul rezonanței, adică la. schimbare de fază (apariția fazei de răsturnare). Cu o creștere ulterioară când. schimbarea schimbării de fază apare lent în intervalul de timp.
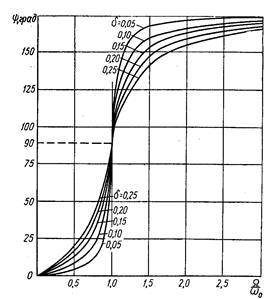
Fig. 5.6 Caracteristicile fazei oscilațiilor amortizate
Factorul de atenuare afectează schimbarea de fază după cum urmează:
- la. tinzând la zero, curbele tind către o curbă limită având o discontinuitate în momentul rezonanței;
- cu creșterea fazei de schimbare în interval este mai rapidă și în intervalul este mai lent.
Dacă coeficientul este mic și frecvența oscilațiilor forțate este mult mai mare decât frecvența oscilațiilor naturale. atunci unghiul de deplasare a fazei se apropie de 180 ° (Figura 5.5 d). Aceasta din urmă este urmată și de ecuația (5.13), în care numitorul devine negativ și, prin urmare, excentricitatea trebuie să fie și negativă. Repetarea probei pentru viteza unghiulară este mai mare decât valoarea critică (), ca în cazul în care ajungem
Rezultă că, pe măsură ce viteza unghiulară crește, deformarea scade, devenind egală cu excentricitatea. În consecință, vitezele de rotație apropiate de cele critice sunt periculoase pentru turbină. La o viteză suficient de îndepărtată în ambele direcții de viteza critică, arborele turbinei funcționează fără vibrații.
În turbinele cu abur sunt utilizate așa-numitele arbori rigizi și flexibili.
Un arbore rigid este unul care are o viteză de operare (frecvența oscilațiilor forțate), dar una flexibilă, care are o viteză de funcționare mai mare decât cea critică.
Arborii de la unitățile moderne puternice de turbină sunt flexibili. La pornirea unei turbine cu un arbore flexibil pentru a împiedica dezvoltarea oscilațiilor rezonante, este necesară trecerea frecvenței critice de rotație într-o perioadă scurtă de timp. Pentru funcționarea silențioasă a arborelui, viteza de operare trebuie să difere de cea critică cu cel puțin 20 ... 30%. Viteza critică pentru arborii flexibili nu trebuie să fie diferită de cea de lucru, deoarece poate avea loc un al doilea ton de oscilații la frecvența de operare de rotație.
În turbinele cu viteză variabilă, se folosesc de obicei arbori rigizi, viteza critică a căror viteză critică este de 20 ... 30% sau mai mare deasupra vitezei maxime de operare.
Luați în considerare oscilațiile arborelui orizontal din Fig. 5.7. Sub influența gravitației discului. orientat în jos, arborele se îndoaie de cantitatea de deformare statică. Centrul de greutate este situat la o distanță de axa arborelui. Când arborele se rotește cu o viteză unghiulară (mai puțin critică), se formează forța centrifugală. determinând deformarea acestuia și îndreptată de-a lungul razei din centru, astfel încât rotația arborelui să aibă loc în jurul liniei elastice (Figura 5.7b).
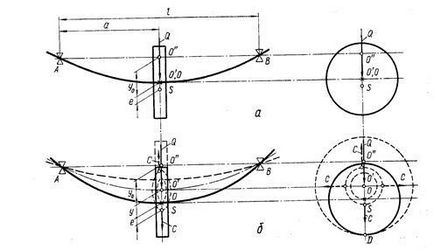
Fig. Poziția centrului de greutate al arborelui orizontal
În Fig. 5.7 b prezintă traiectoriile punctelor. precum și forța centrifugă în cele patru poziții ale centrului de greutate când arborele se rotește cu 90 °. În acest caz, centrul de greutate descrie un cerc cu o rază. prin urmare, ca și în cazul unui arbore vertical.
Această forță este echilibrată de forța elastică. Rezultă că toate concluziile făcute pentru arborele vertical se extind spre arborele orizontal, iar valoarea vitezei unghiulare critice nu depinde de amplasarea arborelui.
Cele de mai sus sunt susținute de poziția lui Stodol că deformarea arborelui sub acțiunea masei discului nu afectează viteza critică de rotație, care rămâne neschimbată în poziția verticală și orizontală a arborelui. Să găsim relația dintre deviația statică și frecvența critică de rotație. Deformarea statică poate fi definită ca
Înlocuind valoarea din (5.12), obținem (c-1)
Astfel, frecvența critică de rotație variază invers cu rădăcina pătrată a deviației statice a arborelui, adică cu deformarea crescătoare a arborelui scade într-un pătrat.
Deformarea statică depinde de rigiditatea rotorului, de lungimea arborelui, de metoda de fixare a capetelor și de natura distribuției sarcinii. În cazul general, ecuația statică de deformare în conformitate cu ecuațiile de rezistență materială poate fi scrisă ca
unde - coeficientul, în funcție de metoda de fixare a capetelor arborelui și natura sarcinii; - lungimea arborelui; - momentul inerției arborelui.
De exemplu, pentru un arbore așezat liber pe două suporturi cu o sarcină în mijloc; cu un disc situat la distanță de suport (Figura 5.7a).
În conformitate cu punctul 5.17, devierea statică a arborelui și, prin urmare, frecvența critică de rotație (5.16) depinde în mare măsură de lungimea arborelui, deoarece deformarea sa este proporțională cu cubul de lungime. La calcularea vitezei critice, valoarea necesară poate fi obținută prin schimbarea diametrului arborelui.
Momentul de inerție al arborelui
În consecință, deformarea statică a arborelui și, prin urmare, viteza critică de rotație depind în mod semnificativ de diametrul său. De exemplu, dacă diametrul arborelui este dublat, deformarea va scădea de aproximativ 16 ori, iar viteza critică (5.16) va crește de aproximativ patru ori.
Viteza critică a unui arbore de secțiune constantă cu
masa distribuită uniform
Arborele unei secțiuni constante cu o masă distribuită uniform pe lungime (pentru) se rotește, având o deformare. Pentru a determina frecvența sa critică, vom folosi ecuația diferențială a oscilațiilor tijei prismatice, care va fi scrisă sub forma
Aici este viteza unghiulară de rotație; - masa unei unități de lungime a arborelui.
Soluția generală a ecuației diferențiale (5.18), care conține patru constante arbitrare, are forma
Ținând cont de condițiile limită pentru arborele, situată liber pe două suporturi, obținem un sistem de ecuații omogene, soluția simultană, care sunt determinate de constante arbitrare:
Ecuația (5.21) este satisfăcută dacă
Din expresiile (5.19) și (5.20) obținem formule pentru determinarea vitezei unghiulare critice:
unde este masa unei unități de lungime; - masa întregului corp.
Ecuația finală pentru linia elastică a arborelui se obține din (5.20) cu
În consecință, linia elastică cu oscilații ale unui arbore fără greutate fără discuri este un sinusoid. Cu oscilații:
a) Primul ton - arborele nu are punct nodal (figura 5.8 a);
b) Al doilea ton - pe axul arborelui se află un punct nodal și două jumătăți de undă (Fig.5.8b);
c) Al treilea ton - există două puncte nodale și trei jumătăți de undă (Fig.5.8c).
Spre deosebire de cazul unui arbore fără greutate cu un disc, considerat anterior, un număr infinit de mari de viteze critice este obținut pentru un arbore cu secțiune constantă cu o masă uniform distribuită. Raportul dintre vitezele critice de rotație pentru diferitele oscilații ale arborelui considerat în conformitate cu punctul 5.24 este:
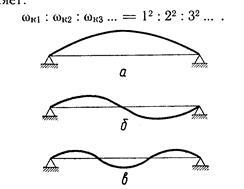
Fig. 5.8 Diferite forme de vibrații ale unui arbore fără greutate fără discuri:
a - tonul 1; b - al doilea ton; c - al treilea ton
Viteza critică
unde este forța de gravitație a arborelui, N; m / s 2.
Deformarea arborelui sub acțiunea unei sarcini statice din masa proprie
Luând în considerare (5.25) și (5.26), obținem