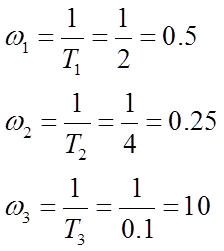Verificarea sistemului de control automat pentru stabilitate prin metoda Hurwitz
1) Funcția de transfer a ACS în stare închisă:
Declarația criteriului Hurwitz:
Pentru stabilitatea ACS este necesar și suficient ca toți minorii diagonali ai determinantului Hurwitz să fie pozitivi.
2) Să găsim ecuația caracteristică a unui sistem dat
Punem la zero numitorul funcției de transfer:
Denumim coeficienții ecuației și le găsim valorile:
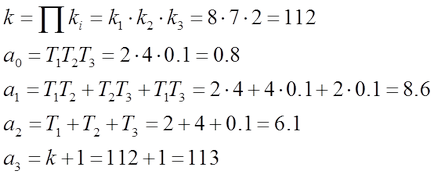
Ecuația caracteristică a unei forme închise va fi:
3) Scriem determinantul Hurwitz:
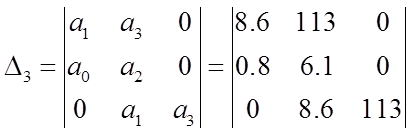
pentru că , atunci concluzionăm că sistemul dat este instabil.
4) Definiți efectul parametrilor sistemului asupra stabilității acestuia.
Calculăm valorile limită ale parametrilor sistemului u:
În acest scop, scriem condiția pentru găsirea unui ACS dat pe limita de stabilitate
Să exprimăm valoarea dorită:
Luăm parametrul drept necunoscut și notăm condiția limită de stabilitate:
Deschidem parantezele și rezolvăm ecuația quadratică rezultată
(în lucrarea de laborator pe care am folosit-o)
Pentru a determina efectul acestui parametru asupra stabilității unui ACS dat, este necesar să se investigheze în continuare stabilitatea sistemului cu scăderea și creșterea acestui parametru în raport cu valorile limită ale acestuia.
Verificarea ACS pentru stabilitatea Nyquist
Criteriul de stabilitate Formularea Nyquist: dacă sistemul buclă deschisă este stabilă, atunci stabilitatea unui sistem închis este necesar și suficient ca APFC buclă deschisă la schimbări w de la zero la ∞, care nu sunt acoperite cu coordonatele punctului (-1; i0).
AFCX cu buclă deschisă are forma:
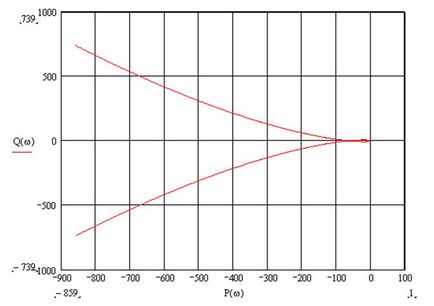
Prin forma de dependență pot spune. Că sistemul deschis este instabil și, prin urmare, închis.
3. Verificarea experimentală a rezultatelor.
3.1) Pentru un ACS dat, eliminați graficul funcției de tranziție și determinați stabilitatea sistemului de tipul acestuia.
Schema de structură cu parametrii dat are forma (în programul MATCAD):
Răspunsul tranzitoriu al unui ACS dat are următoarea formă:
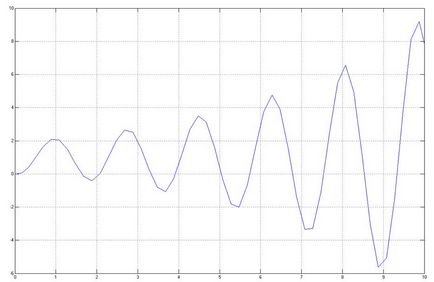
3.2) Investigarea influenței coeficientului de transmisie asupra stabilității sistemului: determinarea (experimentală) a valorii limită a coeficientului de transmisie și identificarea regiunilor de stabilitate (instabilitate). Pentru a elimina graficele funcțiilor tranzitorii ale modurilor de funcționare stabile și instabile și limita de stabilitate.
Să schimbăm valoarea unuia dintre coeficienții dat: let, atunci caracteristica de tranziție are și forma:
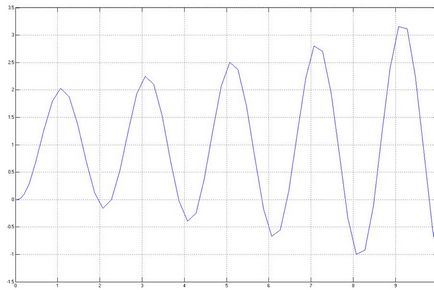
Să presupunem că atunci caracteristica de tranziție are și următoarea formă:
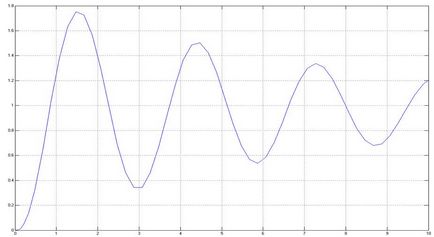
Selectând K în același mod, descoperim că acesta este egal cu 1,15, în timp ce coeficientul de transmisie al sistemului închis este:
Cu un astfel de coeficient de transmisie al unui sistem închis, caracteristica de tranziție are forma:
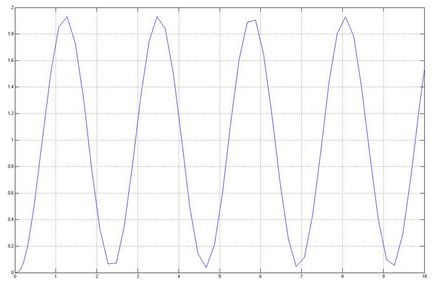
Concluzionăm că UAT este situat pe limita de stabilitate și în regiunea de stabilitate.
3.3) Alinierea model de transport și valoarea de referință a investiga efectul de stabilitate în timp constantă coeficientul sistemului: determinarea valorilor limită ale constantei de timp, și pentru a găsi regiunea de stabilitate (instabilitate). Pentru a elimina graficele funcțiilor tranzitorii ale modurilor de funcționare stabile și instabile și limitele de stabilitate.
Pentru o valoare dată a constantei de timp, caracteristica de tranziție are forma:
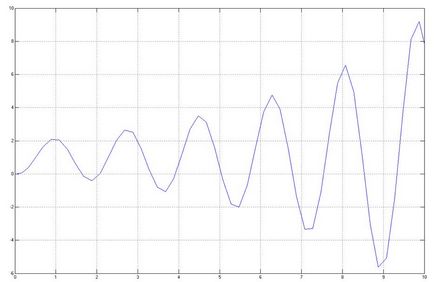
Schimbăm valoarea pe partea mare și cea mai mică și eliminăm caracteristicile tranzitorii:
Să fie 0.15, atunci
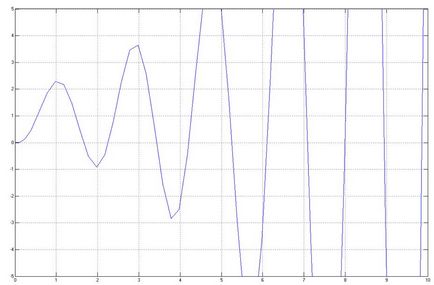
Fie ca valoarea să fie de 0,055, atunci
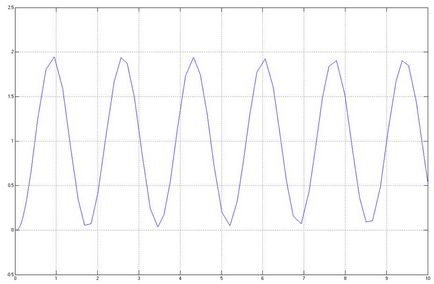
sistemul este la limita de stabilitate, deci este egal cu 0,057
Dacă luăm valoarea mai mică a T, atunci caracteristica de tranziție va fi stabilă, ceea ce înseamnă că regiunea de stabilitate. Să presupunem că T = 0,03.
Graficul grafic al caracteristicii de tranziție va avea apoi forma:
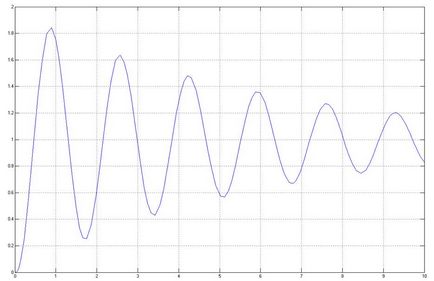
Caracteristica de tranziție este stabilă, prin urmare regiunea de stabilitate este indicată corect.
Trebuie remarcat faptul că există o altă zonă de stabilitate obținută teoretic, care va fi scrisă ca:
3.4) Pentru a elimina caracteristicile de frecvență A (ω) și φ (ω) pentru ACS date în stare deschisă și de la ele pentru a verifica stabilitatea sistemului prin criteriul Nyquist. Atunci când se elimină caracteristicile de frecvență, este obligatoriu să se ia frecvența de conjugare a legăturilor.
Punem sursa semnalului armonic pe intrarea sistemului deschis, în timp ce diagrama structurală ia forma:
Prin schimbarea frecvenței sursei ω, se elimină dependențele A (ω) și φ (ω), datele se înregistrează în tabel:
Frecvențele conjugării legăturilor care intră în ACS sunt egale