Titlul lucrării: Investigarea stabilității sistemelor de comandă automată liniară
Specializare: Comunicare, Comunicatii, Electronica Radio si Dispozitive Digitale
Descriere: Răspunsul pas de control automat într-o stare închisă într-o formă grafică din graficul răspunsului tranzitoriu al sistemului poate observa clar că sistemul cu parametrii menționați este instabilă. Frecvența și caracteristicile pulsului procesului: Amplitudine logaritmică-frecvență și caracteristici de fază-frecvență.
Mărime fișier: 860.5 KB
Lucrarea a fost descărcată: 25 de persoane.
PRACTICA LABORATORĂ
Disciplina: "Sisteme de control al proceselor chimico-tehnologice"
Titlul: "Investigarea stabilității sistemelor de control automat liniar"
Folosind metoda modelării structurale (bazată pe utilizarea matematică a sistemului matematic MatLab sau MathCAD) pentru a investiga sistemul de control automat stabilit pentru stabilitate. Determinarea influenței parametrilor sistemului asupra stabilității acestuia și determinarea valorilor sale limită (critice).
DATE INIȚIALE (6 OPȚIUNI):
Pentru un anumit ACS, eliminați graficul funcției de tranziție și determinați stabilitatea sistemului de tipul acestuia.
Diagrama structurala a acestui ACS in stare inchisa.
Modelul Simulink al acestui ACS în stare închisă în "MATLAB":
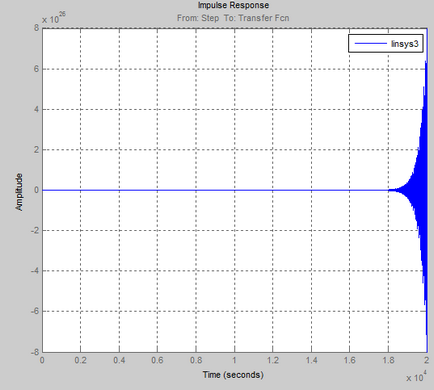
Răspunsul tranzitoriu al ACS într-o stare închisă într-o formă grafică:
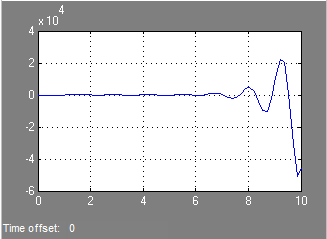
Din graficul răspunsului tranzitoriu al sistemului se vede clar că sistemul dat pentru parametrii instabili este instabil.
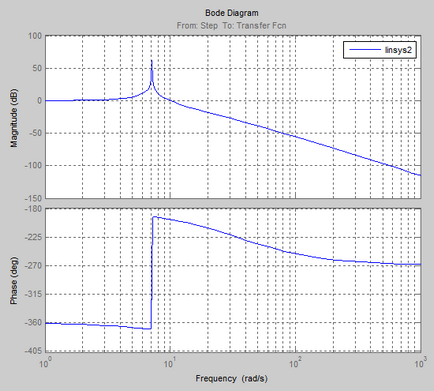
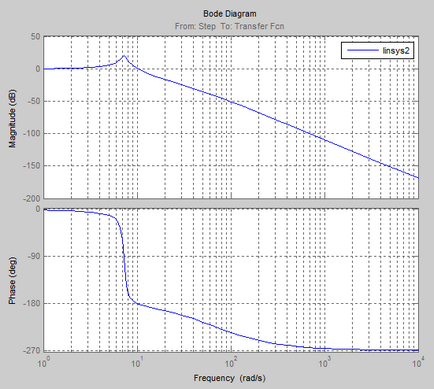
Frecvența și caracteristicile impulsului procesului:
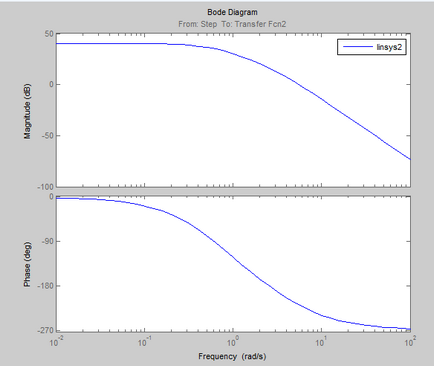
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
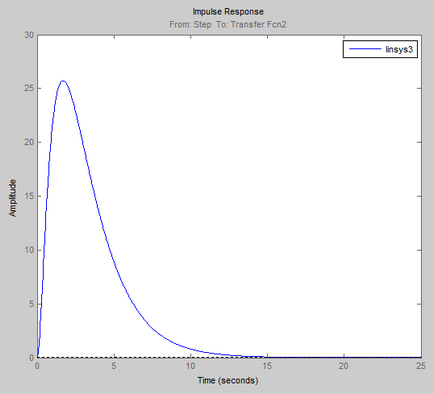
Determinarea stabilității sistemului de control automat prin criteriul Hurwitz.
Criteriul Hurwitz # 150; Acesta este un criteriu sub forma unui determinant, care este alcătuit din coeficienții ecuației caracteristice.
Funcția de transfer a ACS (în stare închisă):
Funcția de transfer a ACS dat (în starea închisă).
condiție necesară și suficientă pentru stabilitatea sistemului de control automat, astfel încât atunci când un 0 0, toți minorii diagonale ale determinanților Hurwitz au fost pozitive.
Să găsim ecuația caracteristică a unui sistem dat.
Punem la zero numitorul funcției de transfer a ACS dat:
Noi deschidem paranteze, dăm altele similare și notăm ecuația caracteristică în forma recepționată pentru scriere:
Denumim coeficienții ecuației și le găsim valorile:
În notația adoptată, ecuația caracteristică va avea forma:
Se compune determinantul Hurwitz, se notează condițiile de stabilitate și se determină stabilitatea UAT.
Reguli pentru compilarea determinantului:
- Coeficienții ecuației caracteristice sunt scrise de-a lungul diagonalei principale, începând cu un 1,
- Coloanele din tabel, din diagonala principală sunt umplute coeficienți din ecuația caracteristică cu indicii în creștere în scădere în jos,
- Toți coeficienții cu indici mai mici de zero și mai mari decât n sunt înlocuiți cu zerouri (n # 150; gradul ecuației caracteristice).
Să verificăm ACS pentru aceste condiții:
Acest ACS nu este stabil, deoarece nu sunt îndeplinite condițiile criteriului de stabilitate.
Instabilitatea acestui sistem automat de control poate fi văzută nu numai în funcție de grafic, ci și în funcție de criteriul lui Hurwitz.
- Investigați efectul factorului de transmisie (=) asupra stabilității sistemului: determinați valoarea coeficientului de transmisie () și găsiți regiunea de stabilitate (instabilitate). Pentru a elimina graficele funcțiilor tranzitorii ale unui mod de funcționare stabil și instabil și limita de stabilitate.
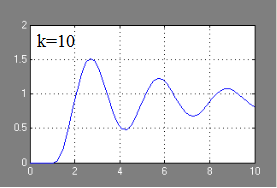
Efectul coeficientului de transmisie k asupra formei răspunsului tranzitoriu și a proprietății acestui ACS.
Modelul Simulink al acestui ACS în "MATLAB" pentru diferite valori ale lui k.
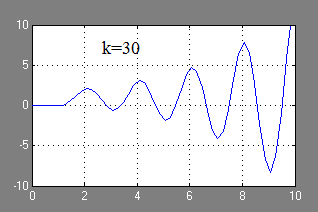
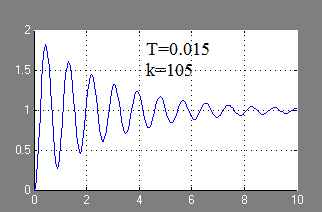
Efectul coeficientului de transmisie k. privind răspunsul tranzitoriu al ACS:
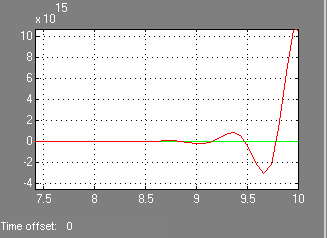
Cu o creștere a coeficientului de transmisie k, frecvența și amplitudinea oscilațiilor sistemului instabil cresc.
Frecvența și caracteristicile impulsului procesului:
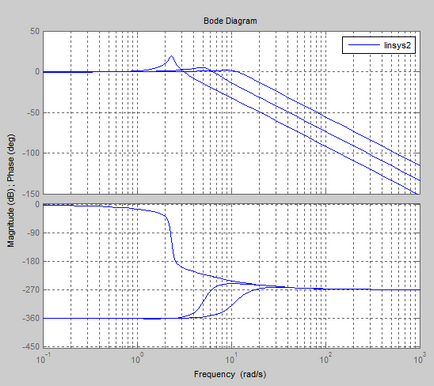
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
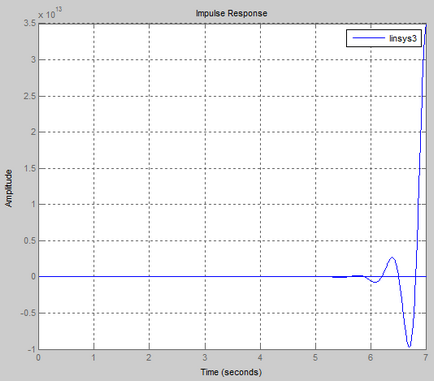
Coeficientul de transfer k are o valoare limită, iar atunci când valoarea lui k scade în raport cu valoarea limită, sistemul este stabil, iar atunci când crește, este instabil.
Regiunea de stabilitate a sistemului în intervalul de la 0 la .
Determinarea valorii limită a coeficientului de transmisie k g.
Condiția pentru găsirea unui ACS dat pe limita de stabilitate ()
Deoarece am ajuns la concluzia că sistemul nu este stabil.
Diagrama structurala a acestui sistem automat de control la limita de stabilitate.
Simulink-model al acestui sistem automat de control la limita stabilității în "MATLAB":
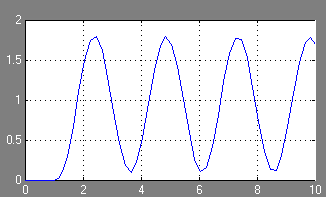
Caracteristica tranzitorie a acestui sistem automat de control la limita de stabilitate într-o formă grafică:
Frecvența și caracteristicile impulsului procesului:
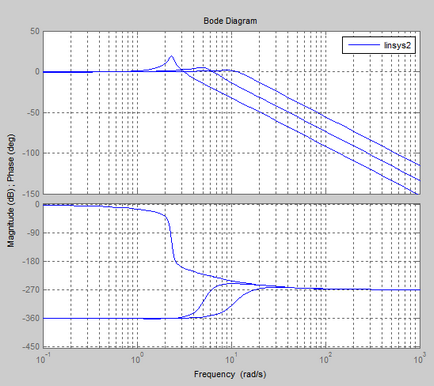
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
Examinarea unui ACS dat sub condiție
Diagrama structurala a acestui ACS la.
Simulink-model al acestui sistem automat de control în "MATLAB":
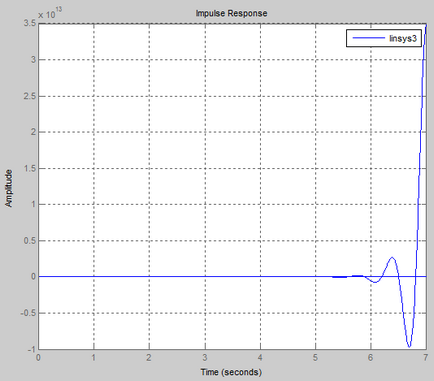
Răspunsul tranzitoriu al acestui sistem automat de control în formă grafică:
Din graficul răspunsului tranzitoriu este clar că sistemul este stabil.
Frecvența și caracteristicile impulsului procesului:
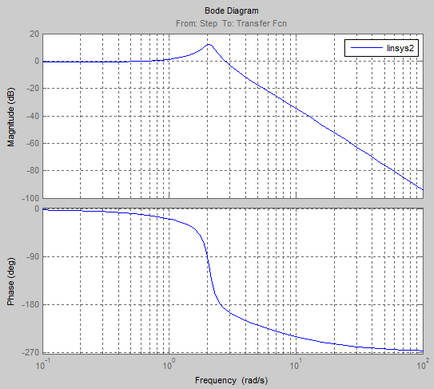
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
Examinarea unui ACS dat sub condiție
Diagrama structurala a acestui ACS la.
Simulink-model al acestui sistem automat de control în "MATLAB":
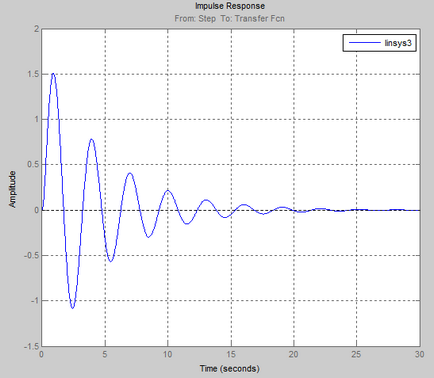
Răspunsul tranzitoriu al acestui sistem automat de control în formă grafică:
Din graficul caracteristicii tranzitorii se observă că sistemul este instabil.
Frecvența și caracteristicile impulsului procesului:
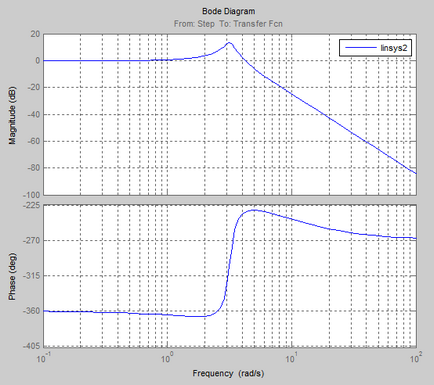
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
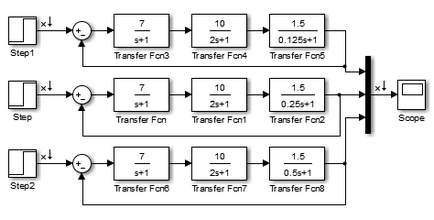
- Alinierea modelului valorii de referință influențează constanta de timp a coeficientului de transmisie T 3 și pentru a investiga stabilitatea sistemului: determinarea valorilor limită ale T 3 constante de timp și pentru a găsi regiunea de stabilitate (instabilitate). Pentru a elimina graficele funcțiilor tranzitorii ale modurilor de funcționare stabile și instabile și limitele de stabilitate.
Influența asupra stabilității sistemului
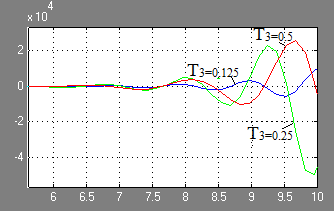
Influența constantei de timp T 3 asupra formei răspunsului tranzitoriu și a proprietății acestui sistem automat de control.
Simulink-model al acestui sistem automat de control în "MATLAB" pentru diferite valori ale T3.
Influența constantei de timp T3 asupra răspunsului tranzitoriu al ACS:
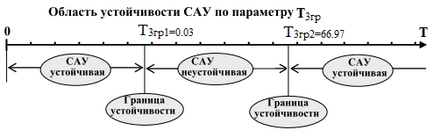
Determinarea valorilor limită ale constantei de timp T 3gr.
Luăm parametrul T 3rp ca necunoscut și notăm condiția limită de stabilitate:
Prin urmare, exprimăm T 3r.
Aceste două valori ale T 3pp caracterizează limita de stabilitate a sistemului de control automat.
Schema structurală a acestui sistem automat de comandă la limita de stabilitate la T 3rp = 66,97.
Modelul Simulink al acestui sistem automat de control la limita de stabilitate la T 3gp = 66.97 în "MATLAB":
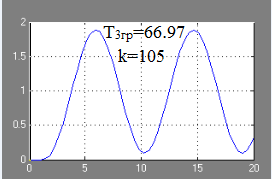
Răspunsul tranzitoriu al acestui sistem automat de control la limita de stabilitate la T 3gp = 66.97 în formă grafică:
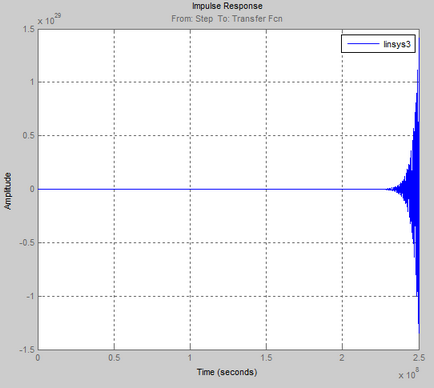
Frecvența și caracteristicile impulsului procesului:
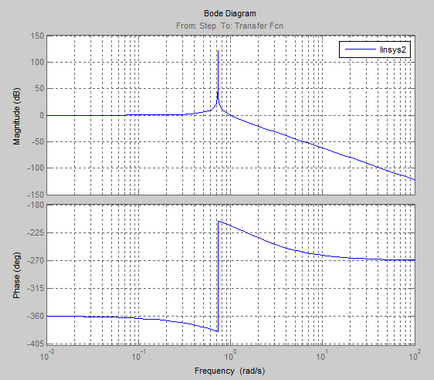
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
Schema structurală a acestui sistem automat de comandă la limita de stabilitate la T 3rp = 0,03.
Modelul Simulink al acestui sistem automat de control la limita de stabilitate la T 3gp = 0,03 în "MATLAB":
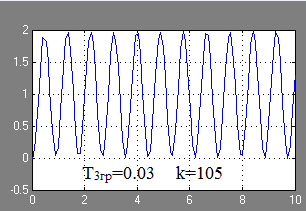
Răspunsul tranzitoriu al acestui sistem automat de control la limita de stabilitate la T 3gp = 0,03 în formă grafică:
Frecvența și caracteristicile impulsului procesului:
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
Examinarea unui ACS dat sub condiție
Diagrama structurala a acestui ACS la.
Simulink-model al acestui sistem automat de control în "MATLAB":
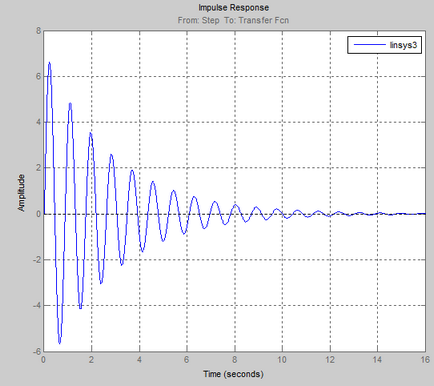
Răspunsul tranzitoriu al acestui sistem automat de control în formă grafică:
La valori ale lui T mai mică decât T3rp1, OPU devine stabilă.
Frecvența și caracteristicile impulsului procesului:
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
Examinarea unui ACS dat sub condiție
Diagrama structurala a acestui ACS la.
Simulink-model al acestui sistem automat de control în "MATLAB":
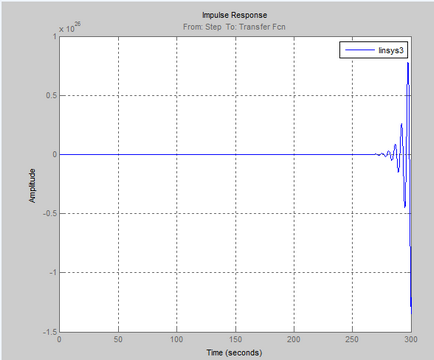
Răspunsul tranzitoriu al acestui sistem automat de control în formă grafică:
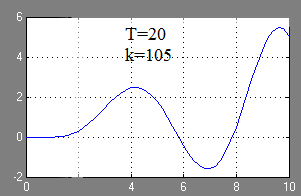
Pentru valorile lui T între cele două valori limită, ACS devine instabilă.
Frecvența și caracteristicile impulsului procesului:
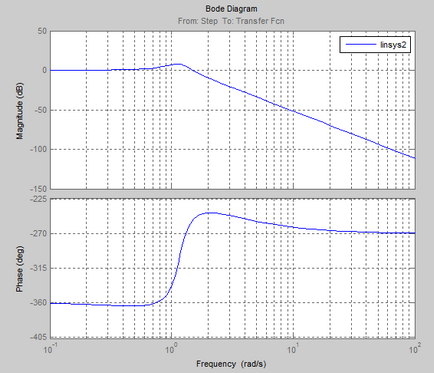
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
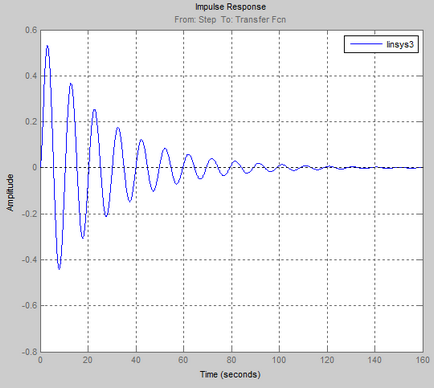
Examinarea unui ACS dat sub condiție
Diagrama structurala a acestui ACS la.
Simulink-model al acestui sistem automat de control în "MATLAB":
Răspunsul tranzitoriu al acestui sistem automat de control în formă grafică:
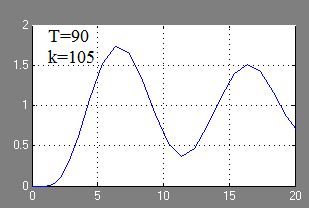
La valori de T, mai mari decât T3rp2, UAS devine stabilă.
Frecvența și caracteristicile impulsului procesului:
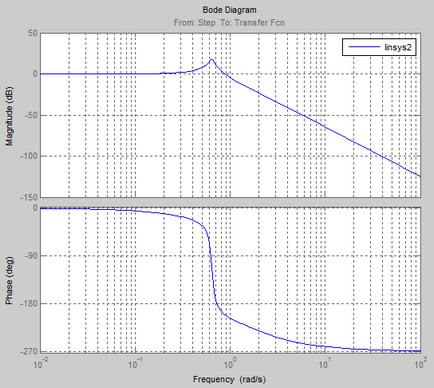
Logaritmica caracteristici de frecvență și amplitudine de fază (LAFCHH)
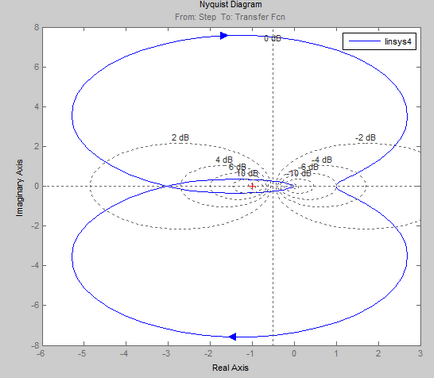
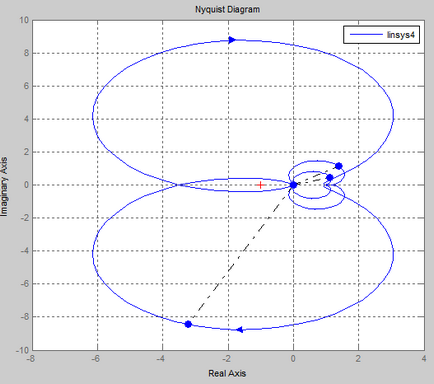
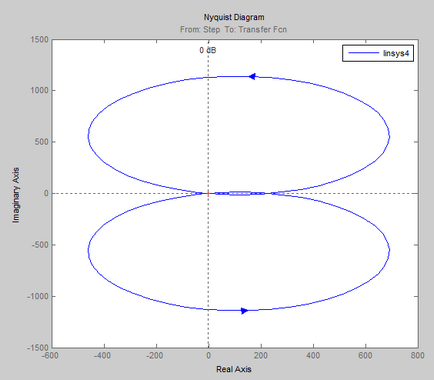
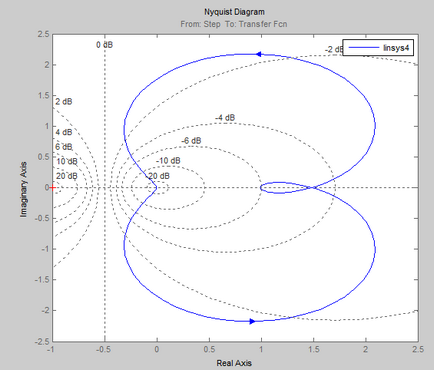
- Eliminați caracteristicile de frecvență pentru un anumit ACS în stare deschisă și pe ele pentru a verifica stabilitatea sistemului prin criteriul Nyquist.
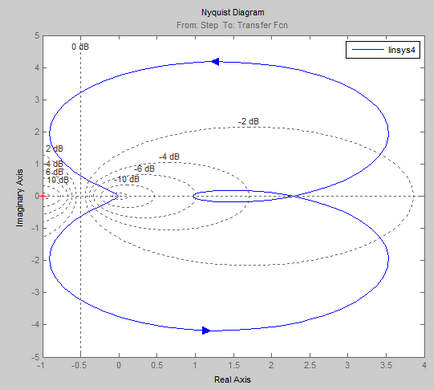
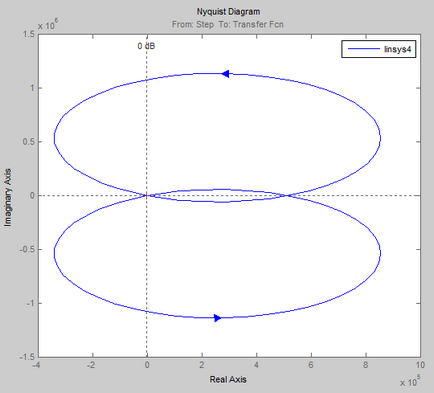
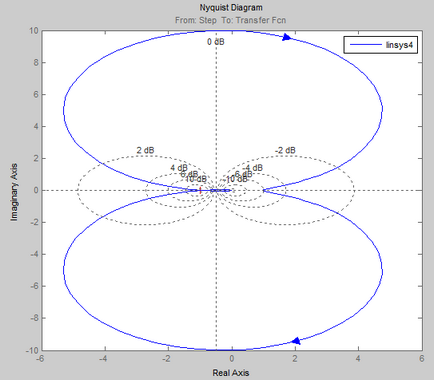
Criteriul de stabilitate Nyquist este destinat să determine stabilitatea sistemelor închise prin caracteristicile de frecvență ale circuitelor deschise echivalente.
Dacă sistemul deschis este stabil, atunci pentru stabilitatea sistemului închis corespunzător este necesar ca AFCX cu buclă deschisă să nu acopere punctul [-1; 0] în planul complex.
Diagrama structurala a acestui ACS in stare deschisa.
Modelul Simulink al acestui ACS în stare deschisă în "MATLAB":
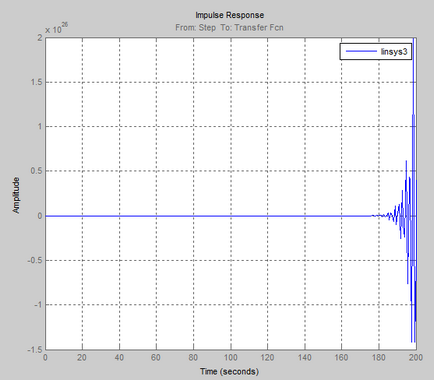
Răspunsul tranzitoriu al ACS în stare deschisă sub formă grafică:
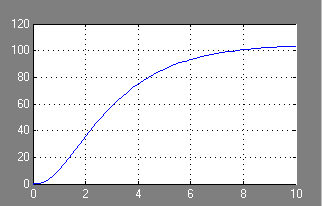
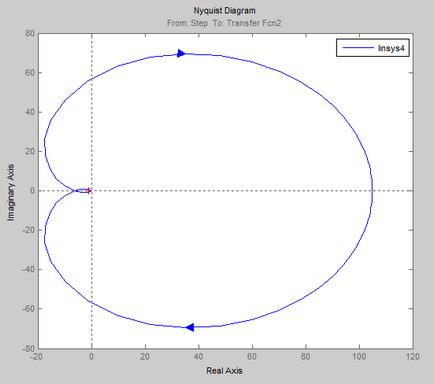
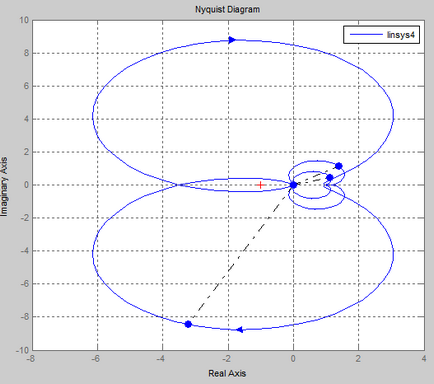
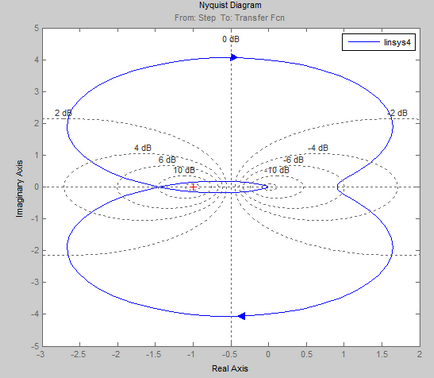
Verificarea stabilității acestui sistem automat de control prin criteriul Nyquist.
În programul Mathcad.
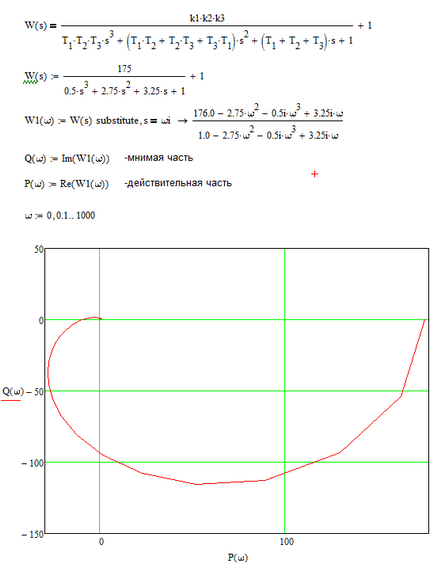
Conform sistemului AFCS obținut, atunci când se trece de la 0 la starea deschisă, se poate concluziona că un sistem de control automat închis # 150; este instabilă, deoarece AFCX acoperă punctul (-1; 0).
Lista literaturii utilizate: