Hyperbola este locusul punctelor planului, pentru fiecare dintre acestea valoarea absolută a diferenței de distanță față de două puncte date ale planului u. numite focare, este o valoare constantă egală cu 2a.
Distanța dintre focuri este 2c.
Dacă axele unui sistem de coordonate dreptunghiulare carteziană sunt alese astfel încât focurile hiperboliei date să fie situate pe axa absciselor simetric față de origine (Figura 2.13.1), atunci ecuația canonică a hiperbolei are forma
În cazul în care. O ecuație a formei (2.13.1) este numită ecuația canonică a unei hiperbola. Cu această alegere a sistemului de coordonate, axele de coordonate sunt axele de simetrie ale hiperbolei. iar originea este centrul ei de simetrie. Axa Ox este numită axa reală. și Oy este axa imaginară a hiperboliei. Punctele de intersecție a hiperboliei cu axa sunt numite vârfurile hiperboliei.
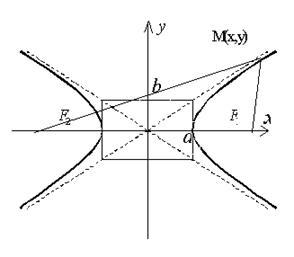
Dreptunghi cu laturile 2a și 2b. situată simetric în raport cu axele hiperboliei și atingând-o la vârfuri, se numește dreptunghiul de bază al hiperboliei. Diagonalele dreptunghiului de bază (fără limitare continuă) sunt asimptotele hiperboliei și sunt definite de ecuații
Excentricitatea hiperboliei (precum și elipsa) este numărul. unde a este distanța de la centrul hiperboliei până la vârful ei. Este evident că pentru orice hiperbolă e> 1.
Dacă M (x; y) este un punct arbitrar al hiperboliei, atunci segmentele u se numesc razele focale ale punctului M. Radiologia focală a ramificației drepte a hiperbolei poate fi calculată prin formulele și. Raza focală a ramurii stângi a hiperbola - conform formulelor și.
Dacă hiperbola este dată de ecuația (2.13.1), atunci liniile definite de ecuații. se numesc direcțiile sale directe.
Ecuația unei hiperbolă a cărei focare se află pe axa absciselor este simetrică în raport cu originea dacă punctul se află pe hiperbola și ecuațiile asimptote sunt cunoscute.
Din ecuațiile pentru asimptote găsim. sau. Deoarece punctul aparține hiperbolei, coordonatele sale satisfac ecuația (2.13.1) :. unde sau. De aici găsim. atunci. prin urmare, ecuația hiperbola are forma.
Hiperbola este dată. Găsiți semiaxurile a și b. se concentrează, excentricitatea, ecuațiile asimptote.
Împărțim ambele părți ale acestei ecuații cu 144. Obținem. Prin urmare, a = 3, b = 4, prin urmare, axele hiperboliei sunt respectiv 2a = 6 și 2b = 8. Deci, cum. apoi focurile hiperboliei sunt la punctele și. Excentricitatea hiperboliei este calculată prin formula. În conformitate cu (2.13.2), ecuațiile asimptote au forma :.
Parabola, directorul ei
O parabolă este locusul punctelor unui plan, pentru fiecare dintre acestea distanța față de un punct fix al planului F. se numește focalizare. este egală cu distanța către o anumită linie fixă, numită directrix.
Să fie dată o parabolă. Introducem un sistem de coordonate dreptunghiular cartesian astfel incat axa abscisa sa treaca prin focalizarea parabolei date perpendicular pe directia directa si este directionata de la directia directa spre focus. Porniți coordonatele la mijloc între focalizare și regizor (figura 2.14.1). În acest sistem de coordonate, această parabolă va fi determinată de ecuația:
unde p este distanța de la focalizare la direcția directă (parametrul parabola). Ecuația (2.14.1) este ecuația canonică a unei parabole.
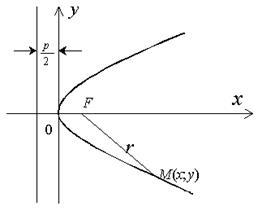
Direcțiunea directă a unei parabole date este determinată de ecuație. Raza focală a unui punct arbitrar M (x; y) al unei parabole poate fi calculată din formula
O parabolă are o axă de simetrie, numită axa parabolului, cu care se intersectează la un singur punct. Punctul în care parabola intersectează axa simetriei se numește vârful parabolei. Cu alegerea de mai sus a sistemului de coordonate, axa parabolei este aliniată cu abscisa, vârful este la origine, iar întreaga parabolă se află în jumătatea dreaptă.
Dacă vârful parabolei (2.14.1) este transferat la un punct. atunci ecuația canonică ia forma.
Găsiți focalizarea F și ecuația direcției directe a unei parabole.
Parametrul acestei parabole este p = 12. Deoarece distanța de la focalizare la director este. atunci focalizarea are coordonatele F (6; 0). dar ecuația direcției directe. adică, x + 6 = 0.
Scrieți ecuația parabolei cu vârful la origine și focalizarea la punctul F (0; 8).
Deoarece focalizarea parabolei se situează pe axa ordinii, iar vârful ei este la origine, ecuația parabolei poate fi scrisă în formă. Deoarece ordonata focusului este negativă, ecuația parabolei trebuie căutată sub formă.
Distanța focală. de unde 2p = 32. În consecință, ecuația parabolică are forma.