Soluția ecuațiilor neliniare
Să luăm în considerare, cum pe o foaie de lucru prin selectarea parametrilor este posibil să se găsească rădăcini ale ecuației cu un singur argument. Ca exemplu de bază, luați în considerare următoarea ecuație:
x 3 - 0,01x 2 - 0,7044x + 0,139104 = 0.
Din moment ce căutăm rădăcinile unui polinom de gradul trei, atunci nu mai sunt mai mult de trei rădăcini reale.
Pentru a găsi rădăcinile, trebuie mai întâi să fie localizate, adică să găsească intervalele la care există aceste rădăcini. Astfel de intervale de localizare a rădăcinilor pot fi intervale, la capetele cărora funcția are semnul opus. Pentru a găsi intervale la a căror limită funcția schimbă semnul, este necesar să-și construiască programul sau să-l tabuleze. De exemplu, vom tabula polinomul nostru pe intervalul [-1; 1] în pași de 0,2. În acest scop:
1. Introduceți o valoare de -1 în celula A2 și valoarea -0,8 în celula A3.
2. Selectați intervalul A2: A3, poziționați indicatorul mouse-ului pe marcatorul de umplere al acestui interval și trageți-l în gama A4: A12. Argumentul este tabelat.
3. În celula B2, introduceți formula:
= A2 ^ 3-0,01 * A2 ^ 2-0,7044 * A2 + 0,139104
4. Selectați celula B2. Așezați indicatorul mouse-ului pe umplutura acestei celule și trageți-l în intervalul B3: B12. Funcția este de asemenea în tabel.
În Fig. 1 că semnul schimbă polinomul pe intervalele [-1; -0,8], [0,2; 0,4] și [0,6; 0,8] și, prin urmare, fiecare dintre aceste intervale are propria rădăcină. Întrucât un polinom de gradul trei nu are mai mult de trei rădăcini, toate sunt localizate.
Înainte de a începe să găsiți rădăcinile prin selectarea unui parametru, trebuie să faceți niște lucrări pregătitoare:
- Setați precizia cu care este localizată rădăcina. Rădăcina poate fi găsită prin metoda aproximărilor succesive cu ajutorul selecției parametrilor. Pentru a face acest lucru, selectați Instrumente → Opțiuni și în fila Calcule din caseta de dialog Opțiuni, setați eroarea relativă și numărul maxim de iterații la 0.00001 și respectiv 1000
- În foaia de lucru, deplasați celula la rădăcina dorită, de exemplu C2. Această celulă va juca un rol dublu. Înainte de a aplica alegerea parametrului, se găsește în el aproximația inițială la rădăcina ecuației și, după aplicare, valoarea aproximativă a rădăcină găsită.
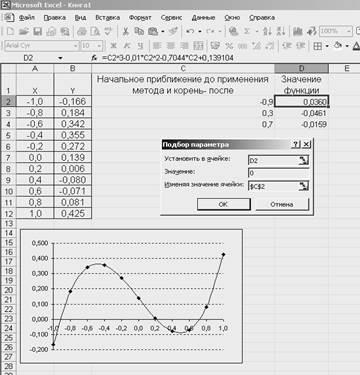
Fig. 1. Localizarea rădăcinilor unui polinom și caseta de dialog Selectarea parametrilor
În mod similar, trebuie să ne ocupăm și de alte două rădăcini dorite:
- Lăsați celula C3 sub a doua rădăcină, introduceți o aproximație inițială de 0,3. iar în celula D3 introduceți următoarea formulă
= C3 ^ 3-0,01 * C3 ^ 2-0,7044 * C3 + 0,139104 - Lăsați celula C4 sub a doua rădăcină, introduceți în ea aproximația inițială de 0,7, iar în celula D4 introduceți următoarea formulă
= C4 ^ 3-0,01 * C4 ^ 2,7044 * C4 + 0,139104
Acum putem începe să găsim prima rădăcină a ecuației:
1. Selectați Instrumente → Selecție parametru. Se afișează caseta de dialog Selectare parametru.
3. În caseta Value data, tastați 0. Aceasta este valoarea din partea dreaptă a ecuației.
5. Faceți clic pe OK.
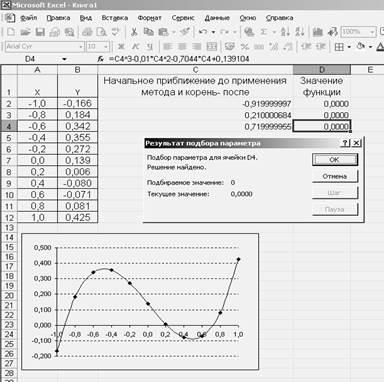
Fig. 2. Toate pe rădăcinile ecuației și caseta de dialog Rezultatul alegerii parametrilor după finalizarea cu succes a căutării celei de-a treia rădăcini.
Notă. Introduceți referințele celulelor în câmpurile din caseta de dialog Selectarea parametrilor este mai convenabilă nu de la tastatură, ci prin selectarea celulei corespunzătoare din foaia de lucru. În acest caz, MS Excel le va transforma automat în link-uri absolute - în cazul nostru $ D $ 2 și $ C $ 2.